Линейные модели для принятия бизнес-решений
Основные понятия моделирования
В процессе жизнедеятельности человека вырабатываются представления о тех или иных свойствах реальных объектов и их взаимодействиях. Эти представления формируются человеком в виде описаний объектов, для которых используются язык описания. Это может быть словесное описание (вербальные модели), рисунок, чертеж, график, макет и т. п. Все перечисленное обобщается одним понятием модель, а процесс построения моделей – моделированием.
Моделирование – это универсальный способ изучения процессов и явлений реального мира. Особое значение моделирование приобретает при изучении объектов, недоступных прямому наблюдению и исследованию. К ним, в частности, относятся социально-экономические явления и процессы.
Изучение любого объекта, любой формы движения – это раскрытие не только его качественных, но и количественных закономерностей, изучаемых математикой. Сказанное в полной мере относится к экономике.
Экономика – это система общественного производства, осуществляющая собственно производство, распределение, обмен и потребление необходимых обществу материальных благ.
Соответственно, экономико-математическая модель – это выраженная в формально-математических терминах экономическая абстракция, логическая структура которой определяется как объективными свойствами предмета описания, так и субъективным целевым фактором исследования, для которого это описание предпринимается.
Экономико-математические задачи в сельском хозяйстве решаются с помощью математических методов. Среди них наиболее разработанными являются методы линейного программирования (ЛП). Такие методы используются для решения экономико-математических задач, в которых количественные зависимости выражены линейно, т.е. все условия выражены в виде системы линейных уравнений и неравенств, а критерий оптимальности – в виде линейной функции, стремящейся к минимуму или максимуму (к экстремуму).
Задача линейного программирования состоит из целевой функции, системы ограничений и условия неотрицательности переменных.
Пусть дана функция n переменных 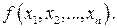 Необходимо найти наибольшее или наименьшее значение этой функции при условии, что аргумент
Необходимо найти наибольшее или наименьшее значение этой функции при условии, что аргумент 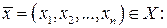
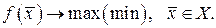
Поставленная таким образом задача оптимизации называется задачей математического программирования. Множество Х называется множеством допустимых решений, а функция 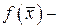 целевой функцией или функцией цели. Допустимое решение
целевой функцией или функцией цели. Допустимое решение 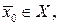 при котором функция принимает наибольшее (или наименьшее) значение, называется оптимальным решением задачи.
при котором функция принимает наибольшее (или наименьшее) значение, называется оптимальным решением задачи.
Если целевая функция 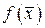 является линейной, а множество Х задается с помощью системы линейных уравнений и неравенств, то задача называется задачей линейного программирования (ЗЛП). Таким образом, общая постановка задачи линейного программирования такова:
является линейной, а множество Х задается с помощью системы линейных уравнений и неравенств, то задача называется задачей линейного программирования (ЗЛП). Таким образом, общая постановка задачи линейного программирования такова:
найти экстремум функции
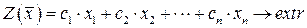
при ограничениях
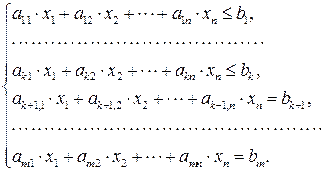
при условиях неотрицательности
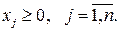
Введем обозначения:
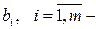 запасы i–го вида ресурса;
запасы i–го вида ресурса;
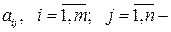 затраты i–го вида ресурса на производство j–го вида продукции;
затраты i–го вида ресурса на производство j–го вида продукции;
 прибыль от реализации единицы j–го вида продукции.
прибыль от реализации единицы j–го вида продукции.
В компактной записи задача линейного программирования имеет вид:
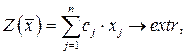
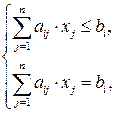
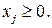
Компактная запись показывает, что модель общей задачи линейного программирования включает пять основных элементов:
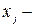 переменные величины, значение которых отыскивается в процессе решения задачи;
переменные величины, значение которых отыскивается в процессе решения задачи;
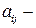 технико-экономические коэффициенты при переменных в ограничениях;
технико-экономические коэффициенты при переменных в ограничениях;
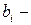 объем правой части неравенств, которые называют константами задачи;
объем правой части неравенств, которые называют константами задачи;
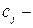 коэффициенты при переменных в целевой функции, которые называют оценками переменных;
коэффициенты при переменных в целевой функции, которые называют оценками переменных;
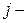 индекс переменной;
индекс переменной;
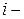 индекс ограничения.
индекс ограничения.
Целевой функцией(функцией цели) называется математическое выражение, для которого требуется найти экстремальное, то есть максимальное или минимальное, значение.
Переменными величинамиxj обозначают такие виды и способы деятельности, размеры которых неизвестны и должны быть определены в ходе решения задачи. Обычно в задачах по сельскому хозяйству переменные величины означают искомые размеры отраслей хозяйства, виды кормов в рационе, марки тракторов и сельскохозяйственных машин и т.д. В соответствии с конкретными условиями одна и та же культура или вид скота могут выражаться нескольким переменными. Например, зерно товарное и фуражное; кукуруза на зерно, силос, зеленый корм; многолетние травы на сено, сенаж, зеленый корм, травяную муку и семена и т.д.
Переменные величины могут произвольно изменяться в условиях рассматриваемой задачи. Переменная, коэффициенты которой образуют единичный столбец, называется базисной. Базисные переменные образуют единичный базис системы. Переменные,не входящие в единичный базис, называются свободными.
Общее количество переменных, включаемых в задачу, определяется характером задачи, конкретными условиями производства, возможностью сбора информации и т.д.
Переменные могут выражаться в самых различных единицах измерения: га, ц, кг, шт., головах и т.д. По характеру переменные подразделяют на основные, дополнительные и вспомогательные. К основным переменным относят искомые виды деятельности: отрасли хозяйства, виды кормов, марки машин. Дополнительными называют переменные, которые образуют в процессе превращения неравенств в уравнения. Они могут означать недоиспользованную часть ресурсов, излишек над правой частью неравенства (если это неравенство типа «не более»). Вспомогательные переменные включают в задачу для того, чтобы определить расчетные величины приобретаемых производственных ресурсов, расчетные величины показателей экономической эффективности производства.
Дополнительные и вспомогательные переменные всегда имеют единичные коэффициенты (+1 или –1).
Технико-экономические коэффициенты (aij) при переменных в системе ограничений выражают нормы затрат производственных ресурсов или норму выхода продукции в расчете на единицу измерения переменной величины.
И в том и в другом случае необходимо, чтобы технико-экономи-ческие коэффициенты точно соответствовали тому периоду планирования, на который решается задача. Например, если задача решается для экономико-математического анализа производства за прошлый период, то коэффициенты будут рассчитываться по отчетным данным. Если же она решается на перспективу, то и коэффициенты должны быть рассчитаны на эту перспективу.
Нормы затрат ресурсов чаще всего определяются по справочникам, они должны быть скорректированы на соответствующие конкретные условия. Коэффициенты выхода продукции рассчитывают на основе плановой урожайности культур и продуктивности животных.
В случаях, когда необходимо предусмотреть заранее определенные соотношения между переменными, технико-экономические коэффициенты представляют коэффициенты пропорциональности. Например, долю сельскохозяйственных культур в севообороте или долю какого-либо корма в общей группе кормов и т.д.
Правой части ограничений (bi) называют константами, т.е. постоянными величинами. К ним относят объемы производственных ресурсов – земли, труда, техники, удобрений, капиталовложений и т.д. Производственные ресурсы должны быть определены с учетом их фактического состояния и обязательно учитывать период планирования. Кроме того, те производственные ресурсы, использование которых в течение года неравномерно, рассчитывают не только за год в целом, но и по отдельным напряженным периодам или месяцам (трудовые ресурсы).
Производственные ресурсы определяют в различных единицах: земельные угодья – в га, трудовые ресурсы – в чел.–днях или в чел.–ч, технику – в количестве машино–смен, сменной или суточной выработки и т.д.
Таким образом, определение наличия производственных ресурсов не простое дело. Необходимо тщательно проанализировать производственную деятельность хозяйства, использование трудовых, земельных, технических и прочих ресурсов, и только после этого включать их объемы в ограничения.
В правой части ограничений отражаются не только количество ресурсов, но и объем производимой продукции по верхнему или нижнему уровню. Нижний уровень показывается в тех случаях, когда заранее известен объем продукции, меньше которого хозяйство не должно производить, а верхний не допускает производство продукции выше определенного объема. Эти ограничения обязательны не всегда. Однако почти ни в одной задаче, предусматривающей определение сочетания отраслей, не обходятся без соответствующих ограничений по продукции, иначе получится однобокое решение. Это связано с тем, что эффективность отраслей неодинаково.
Во всех остальных ограничениях в правой части ставятся нули, так как в них формулируются условия по производству и использованию продукции или отражают ограничения пропорциональной связи.
Ограничение– это математическое выражение, связывающее переменные в виде равенств и неравенств. Все ограничения образуют систему ограничений задачи. Система ограничений в математической форме характеризует условия задачи. Полнота отражения этих условий зависит от состава ограничений. Поэтому при определении количества ограничений необходимо учитывать два обстоятельства:
v отражать в задаче только те условия, которые действительно ограничивают возможности производства;
v слишком большое количество ограничений увеличивает размеры задачи и делает ее трудноразрешимой
Ограничения бывают трех типов: равенства (=), неравенства типа меньше либо равно (≤), неравенства типа больше либо равно (≥). Например,
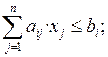
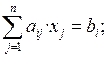

где i = 1, 2, … , m. Коэффициенты при переменных обозначаются aij, где индекс i – номер ограничения, индекс j – номер переменной, свободные члены (правая часть ограничений) обозначаются bi, индекс i – номер ограничения.
Ограничения первого типа называют ограничениями сверху, так как левая часть неравенства не может быть выше определенной величины (константы). Ограничения третьего типа получили название ограничения снизу, так как левая часть неравенства не может быть ниже определенной величины (константы).
По смыслу все ограничения можно подразделить на основные, дополнительные и вспомогательные.
Основные ограничения –это те, которые накладываются на все или большинство переменных задач. Как правило, с их помощью отражаются основные условия задачи – по земле, труду, кормам, питательным веществам, технике и т.д.
Дополнительные ограничениянакладываются на часть переменных величин или на одну переменную. Эти ограничения вводятся в тех случаях, когда необходимо ограничить сверху или снизу размеры отдельных переменных, например, с учетом севооборотных требований или с учетом физиологических пределов насыщения рациона отдельными кормами или их группами. Таким образом, дополнительные ограничения отражают различные возникающие в процессе моделирования дополнительные условия. Но каждое дополнительное ограничение сужает область свободы выбора. Поэтому вводить их в задачу следует осторожно, в разумных пределах и в необходимых случаях.
Вспомогательные ограничения,как правило, самостоятельного значения не имеют и вводятся в задачу для формализации отдельных условий. К ним относятся ограничения, устанавливающие пропорциональную связь между отдельными переменными или их группами.
Оценка переменных в целевой функции (сj) являются коэффициентами, выражающими величину общего дохода или затрат в расчете на единицу измерения переменной. Оценка переменной, как правило, выражает принятый критерий оптимальности. Она может быть представлена и в натуральной, и в денежной форме, т.е. затраты на единицу продукции (себестоимость продукции).
Условие неотрицательности переменных записывается в виде
xj ≥ 0, j = 1, 2, …, n.
В реальной жизни производства, исходя из условий задания, по данной записи структурной экономико-математической модели (ЭММ) составляется перечень переменных величин и ограничений, подготавливается исходная информация, строится развернутая ЭММ задачи, которая затем записывается в виде матрицы (таблицы), вводится в компьютер и по соответствующей программе производится расчет и анализ результатов.
В общем виде задача линейного программирования (ОЗЛП) на максимум записывается так:
Z = 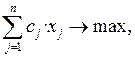 (1.1)
(1.1)
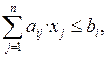 i = 1,…, m,
i = 1,…, m, 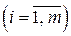 , (1.2)
, (1.2)
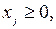 j = 1,…, n,
j = 1,…, n, 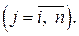 (1.3)
(1.3)
Здесь (1) – целевая функция (максимум прибыли);
(2) – система специальных ограничений на объем фактически име-ющихся ресурсов;
(3) – условие неотрицательности переменных;
xj – переменная.
Задача (1.1) – (1.3) называется задачей линейного программирования в стандартной форме на максимум.
Задача линейного программирования в стандартной форме на минимум имеет вид
 Z =
Z = 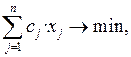 (1.4)
(1.4)
 i = 1, …, m, (1.5)
i = 1, …, m, (1.5)
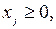 j = 1, …, n. (1.6)
j = 1, …, n. (1.6)
Вектор x = (x1, x2, …, xn), компоненты xj которого удовлетворяют ограничениям (1.2) и (1.3) [или (1.5) и (1.6) в задаче на минимум], называется допустимым решением или допустимым планом задачи ЛП. Совокупность всех допустимых планов называется множеством допустимых планов.
Каноническая форма задачи линейного программирования характерна тем, что содержит целевую функцию, все ограничения равенства, все переменные неотрицательные.
Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности.
Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:
1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;
2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на – 1;
3) если среди ограничений имеются неравенства, то путем введения дополнительных переменных неотрицательных переменных они преобразуются в равенства. Например, дополнительные переменные Sj в ограничения типа меньше либо равно ( £ ) вводятся со знаком плюс:
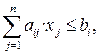

Дополнительные переменные Sj в ограничения типа больше либо равно ( ≥ ) вводятся со знаком минус:
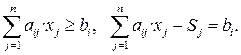
Для устранения отрицательности дополнительных переменных – Sj вводят искусственные переменные со знаком плюс + Мj c очень большими значениями.
Дата добавления: 2015-11-18; просмотров: 2690;
