А. Работа на модели угла.

1. Величины, задаваемые преподавателем: температура внутреннего t_в и наружного t_н воздуха, коэффициенты тепловосприятия α_в, теплоотдачи α_н, теплопроводности λ, толщина ограждения δ = kl_м и относительная влажность f % внутри помещения.

2. Усреднить результаты измерения для симметричных точек и записать в таблицу по форме 2. Расчет температур отдельных точек на модели угла проводят по формуле.

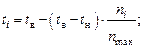(2.1)

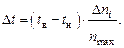
3. Вычертить в масштабе на миллиметровой бумаге схему горизонтальной половины реального угла (не модели) с указанием размеров.

4. Вычислить по формуле (2.1) температуру t_ij и записать ее значение под каждой точкой вычерченной схемы (рис. 2.1).

5. Интерполируя, построить на схеме половины угла (не модели) изотермы (рис 2.2), начиная с минимальной температуры (по указанию преподавателя).

6. Указать зону промерзания угла, начиная от внутренней поверхности стены. Для этого вычертить на схеме угла изотерму:
t = 0 ^оС.

7. Определить точку росы по заданному значению t_в и относительной влажности воздуха f % в помещении [2, c. 45-46].

8. Сделать заключение о влажностном состоянии угла.

9. Вычислить общее термическое сопротивление стены по формуле:

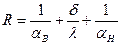
10. Указать, на сколько градусов экспериментальное значение температуры угла ниже температуры внутренней поверхности стены вдали от угла: Δ = t_в.п – t_у. Точки (12.7) и (7.7) – на модели.

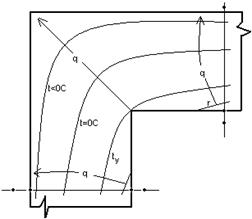
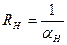
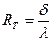
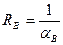
Рис. 2.2. Распределение температур в наружном углу

Б. Аналитические расчетыt_у;t_в.пкак функции отt_н .

1. В одних и тех же координатах на миллиметровой бумаге построить график зависимости t_в.пи t_у от наружной температуры t_н. Аналитически t_в.попределяется по формуле 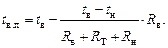(2.2).

(2.2)

2. Аналитическая зависимость t_у = f (t_н) в [4] задается выражением:

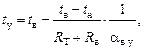(2.3)

где 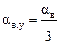- коэффициент тепловосприятия угла.

3. По графику t_у = f (t_н) определить расчетную температуру угла для заданных в работе условий и сравнить с экспериментальным значением. По графику t_в.п = f (t_н) определить расчетную температуру стены для заданных условий и сравнить с экспериментальным значением.

4. По построенным графикам сделать заключение о характере зависимости t_в.п и t_у от наружной температуры t_н. Какой физический смысл несет точка пересечения графиков t_у и t_в.п в зависимости от t_н?

Разность температур t_в.п (стены) и t_у (угла) на основании формул (2.2) и (2.3) может быть рассчитана по формуле:

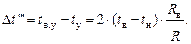
Рассчитать 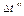и сравнить с полученным на модели. Дать пояснения.

N.B. Конечно, следует помнить, что в настоящее время подавляющее число расчетов в физике строительного дела ведется с использованием компьютерных технологий, компьютерного моделирования.

Контрольные вопросы

1. Какие условия должны выполняться при электрическом моделировании температурного поля наружного угла?

2. Как моделируются граничные условия на поверхностях угла? В чем скажется, если здесь допущено какое-либо отклонение?

3. Какие негативные явления наблюдаются в углах ограждений? Почему?

4. При какой наружной температуре t_н температура угла t_у будет равна температуре внутренней поверхности вдали от угла – t_в.п? Проанализируйте формулы (2.2) и (2.3).

5. Какие меры необходимо принять для исключения негативных явлений (выделение влаги), наблюдаемых в углах ограждений?

Литература

1. СНиП РФ 23-02-2003 «Тепловая защита зданий»; СП 23-101-2004 «Проектирование тепловой защиты зданий».

2. Федорчук Н.М., Грызлов В.С. Избранные главы физики в строительном деле. Учеб. пособие. – Череповец, 1994.

3. Шильд Е.Х., Кассельман Ф., Дамен Г., Поленц Р. Строительная физика. – М: Стройиздат, 1982.