Работа 3

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ТЕПЛОПРОВОДНОГО ВКЛЮЧЕНИЯ НА ТЕМПЕРАТУРНОЕ ПОЛЕ СТЕНЫ (ЭЛЕКТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ)

Цель работы − исследование температурного поля наружной стены с теплопроводным включением; расчеты термических сопротивлений; тепловых потоков.

Оборудование: установка − электрическая модель фрагмента наружной стены с теплопроводным включением.

3.1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ [1]

Указания: перед выполнением данной работы необходимо изучить теоретическое введение к работе 1 «Исследование температурного поля наружной стены методом электрического моделирования».

В реальных ограждающих конструкциях с целью увеличения их устойчивости широко используют введение в материал ограждений различных металлических каркасов, балок. Обычно каркасы и балки изготавливаются из материалов, теплопроводность которых значительно выше по сравнению с обычными материалами (кирпич, легкие бетоны и проч.). В результате введения теплопроводных включений тепловое поле ограждающей конструкции становится неоднородным. Общее тепловое сопротивление ограждения уменьшается. Кроме того, при недостаточном тепловом сопротивлении на внутренней поверхности конструкций в местах теплопроводных включений вероятно выпадение конденсата, что является недопустимым.

Существуют приближенные методы расчета низшей температуры в местах теплопроводных включений, которые разработаны лишь для ограниченных форм конструкций. Для теплопроводного включения, которое исследуется в данной работе, таких методов пока не существует. Поэтому низшую температуру определяют экспериментально с помощью электрической модели.

Для определения приведенного термического сопротивления неоднородной конструкции, изображенной на рис. 3.1, К.Ф. Фокиным был разработан аналитический метод расчета − метод разбиений, суть которого заключается в следующем.

§ Плоскостями, параллельными направлению теплового потока, ограждающая

конструкция условно делится на участки, которые относительно друг друга являются параллельными (рис. 3.2). В данном случае это участки 1, 2 и 3 (рис. 3.2 и 3.3, а). Сопротивление всего фрагмента конструкции определяется в этом случае по формуле:

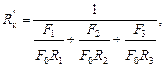(3.1)

где F₁, F₂, F₃ − площади участков 1, 2 и 3 соответственно; R₁, R₂, R₃ − термические сопротивления участков 1, 2 и 3.

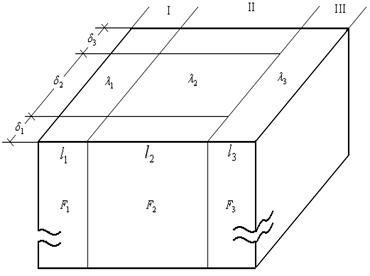
Рис. 3.1. Модель фрагмента неоднородной конструкции

Из рисунка 3.1 видно, что

F₀ = F₁ + F₂ + F₃ = H (l₁ + l₂ + l₃),

где H − высота конструкции (задавать её не обязательно).

Рис. 3.2. Схема разбиения фрагмента неоднородной конструкции

Термическое сопротивление однородного участка (слоя) определяется по формуле:

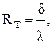, где 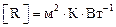(не Омы).

Плоскостями, перпендикулярными к направлению потока тепла, ограждающая конструкция условно разрезается на участки, которые относительно друг друга являются соединенными последовательно. В данном случае это участки I, II и III (смотри рис. 3.2 и 3.3,б). Сопротивление всего фрагмента конструкции тогда определяется по формуле:

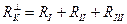(3.2)

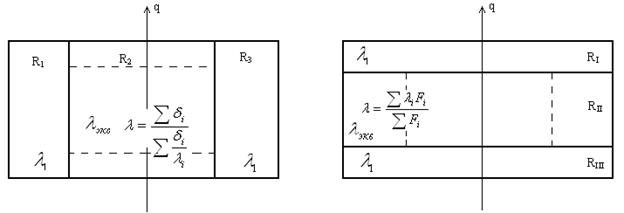
а) б)

Рис.3.3. Сопротивления и коэффициенты теплопроводности участков после разбиения конструкции.

Опыт показывает, что величина 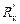, рассчитанная по формуле (3.1), всегда меньше истинного значения сопротивления конструкции, а величина 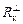, вычисленная по формуле (3.2), соответственно больше этого значения. Поэтому так называемое приведенное термическое сопротивление конструкции рекомендуется определять по формуле:

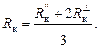(3.3)

При этом предполагается, что в формуле (3.1)

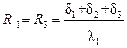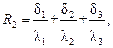, на модели δ₁ = δ₃.

В работе с моделью 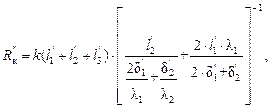(3.5),

где k – коэффициент геометрического подобия «Модель – конструкция»; δ₁, δ₂, δ₁ – толщины участков I, II и III на модели соответственно 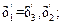λ₁, λ₂ – коэффициенты теплопроводности материалов стены и включения соответственно; l₁ = l₃, l₂ − площади, на модели фрагмента стены соответственно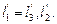

В формуле (3.2):

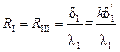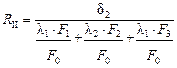; , на модели F₁ = F₃.

В работе с моделью 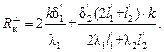(3.5) .

Общее значение термического сопротивления ограждающей конструкции определяется по формуле:

,

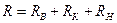где пристеночные сопротивления 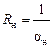, 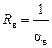(работа 1).

3.2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Электрическая модель фрагмента наружной стены с теплопроводным включением представлена на рисунке 3.4.

Рис.3.4.Электрическая модель фрагмента наружной стены с теплопроводным включением

Модель выполнена из электропроводной графитизированной бумаги. Роль теплопроводного включения играет прямоугольный лист графитизированной бумаги, расположенный в центре модели (заштрихован). Электрическое сопротивление бумаги, имитирующей теплопроводное включение, а также основной материал стены подобраны с соблюдением принципов подобия модели и натуры (см. теоретическое введение к работе 1). Поле модели разбито сеткой. В узлах сетки расположены клеммы 10, к которым при измерении прикасается щуп 11. Ток щупа, создаваемый источником постоянного тока, измеряется гальванометром G. Переменный резистор r служит для задания температурного масштаба (см. далее). Модель конструкции имеет ось симметрии 12. Координаты клемм заданы буквой (со штрихом или без него) и цифрой. Расстояния 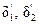и 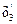показывают толщину отдельных участков на модели, а величины 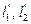и 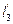− площади. В остальном модель аналогична моделям, используемым в работах 1 и 2.

3.3. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА

1. Касаясь щупом наружной шины 8, включить выключатель К и, меняя сопротивление r, вывести стрелку гальванометра на максимальное деление, т.е. задать температурный масштаб (t_в – t_н ≈ n_max)

2. Касаясь щупом каждой клеммы измерить и записать ток щупа в делениях шкалы (i = A, Б, В, Г, Д, А', Б', В', Г', j = 1, 2, 3, 4, 5, 6, 7). Ввиду того, что модель имеет ось симметрии (12), результаты измерений в симметричных точках рекомендуется усреднить и записать в таблицу в форме 3.1.

Форма 3.1

А′ А
Б′   Б
В′   В
Г′   Г
Д

3.4. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ РЕЗУЛЬТАТОВ

Используя принцип геометрического подобия модели и натурного образца (коэффициент k), рассчитать истинные размеры натурного образца.

В модели 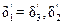; ; 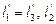λ₂ = 2λ₁.

Величины, задаваемые преподавателем: λ₁, k, t_в, t_н, f %, α_в, α_н − из СНиПа.