ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ МЕТОДОМ ЦИЛИНДРИЧЕСКОГО ЗОНДА

Цель работы: ознакомление с методом цилиндрического зонда при измерении коэффициента теплопроводности строительных материалов и получение навыков экспериментирования по его применению.

Оборудование: цилиндрический зонд-датчик, стабилизированные источники электрического тока, мост сопротивлений, набор образцов строительных материалов, мультиметр С-111.

4.1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ [1]

Передача теплоты твердыми строительными материалами осуществляется в основном за счет теплопроводности в соответствии с дифференциальным законом Фурье:

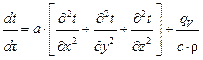, (4.1)

где 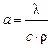, t- температура, τ - время, а - коэффициент температуропроводности, 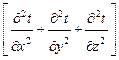- оператор Лапласа, q_V - объемная мощность внутренних источников тепла, 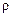- плотность среды, c - удельная теплоемкость среды, λ - коэффициент теплопроводности.

При нестационарном тепловом процессе температура каждой точки среды, по которой распространяется тепловой поток, изменяется по тому или иному закону в зависимости от времени. Поэтому в опытах со стационарными тепловыми процессами обычно измеряется коэффициент теплопроводности λ, а в опытах с нестационарными тепловыми процессами измеряется коэффициент температуропроводности a.

В настоящее время для измерения тепловых характеристик строительных материалов широкое распространение получил метод цилиндрического зонда. Принципиальная блок-схема представлена на рисунке 4.1.

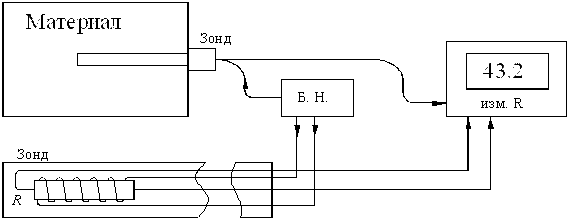
Рис. 4.1. Блок–схема измерительной установки: зонд

Опыт показывает, что данный метод по сравнению с другими обладает рядом существенных преимуществ:

а) для измерения не требуется значительных затрат времени;

б) может использоваться для исследования ограждающих конструкций в процессе их эксплуатации;

в) нестационарный тепловой процесс позволяет определять коэффициент теплопроводности для целого ряда строительных материалов, мало отличающихся друг от друга по теплоемкости и объемному весу.

Теоретической основой для осуществления этого метода, как и всех нестационарных методов, являются частные решения дифференциального уравнения (4.1), которое устанавливает связь между временными 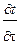и пространственными аΔt изменениями температуры. Для решения уравнения (4.1) должны быть заданы начальные и граничные условия. В случае зонда постоянной мощности решение уравнения (4.1) проводится для бесконечно протяженной среды, внутренне ограниченной металлическим круговым цилиндром, к которому в единицу времени подводится постоянное количество тепла. Решение может быть представлено в виде:

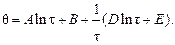(4.2)

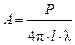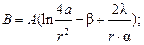
где ; 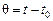- избыточная температура зонда; τ - время нагрева зонда; t₀- температура среды вдали от зонда; P - мощность зонда; l - рабочая длина зонда; α - коэффициент теплообмена на границе «зонд-среда»; r - радиус зонда; β, D, E- постоянные величины, не зависящие от времени. Как следует из уравнения (4.2), по истечении достаточного времени величина 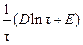будет стремиться к нулю, а переменная 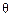становится линейной функцией lnτ. Тогда формула примет вид:

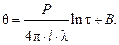(4.3)

Используя линейный участок 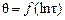для значений τ₁, τ₂ и соответствующих им величин 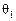и 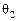, можно получить из уравнения (4.3) выражение коэффициента теплопроводности:

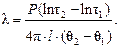(4.4)

4.2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

В экспериментальной установке предусмотрено два способа измерения величины термосопротивления.

Вариант 1 - цифровой осциллограф-мультиметр (рис. 4.2).

Вариант 2 - классическая мостовая схема (рис. 4.3).

Для увеличения чувствительности моста (рис. 4.3) гальванометр Г включен через усилитель тока У. Мощность, подводимая из сети, контролируется вольтметром V, включенным на диапазон измерений 0-30 В, и миллиамперметром А, имеющим диапазон 0-300 мА. Стабилизирующие блоки питания БП₁, БП₂, БП₃ служат для питания соответственно моста и нагревателя зонда.

Цилиндрический зонд (рис. 4.1) состоит из латунной трубки внешним диаметром 4 мм и длиной 180мм , внутри которой смонтирован нагреватель в виде спирали из нихромовой проволоки, намотанной на стеклянный капилляр. В качестве термодатчика служит термосопротивление марки М-172, которое вставлено внутрь капилляра. Для обеспечения жесткости и теплового контакта между отдельными элементами зонда и его корпуса все свободное пространство конструкции зонда заполнено мелким кварцевым песком. Один конец трубки запаян, а на другой конец надета рукоять, сквозь которую выведены соединительные электрические провода от нагревательной спирали и от термодатчика.

4.3. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА

Вариант - мультиметр

Рис. 4.2. Электрическая схема установки (вариант - мультиметр)

1. Ввести зонд в исследуемый материал.

2. Включить мультиметр в сеть и подготовить его к работе в режиме измерителя сопротивлений (в присутствии преподавателя или лаборанта). На экране мультиметра высвечивается значение сопротивления зонда в килоомах.

3. На основной установке включить тумблер Т₆ – «Нагрев» и одновременно пустить в ход секундомер. Об исправности установки можно судить по показаниям амперметра и вольтметра.

4. Выждать время (τ = 24 минуты) выхода режима теплоотдачи зонда на зависимость, задаваемую формулой (4.3).

5. С экрана мультиметра записать в таблицу по форме 4 сопротивление зонда в моменты времени τ = 24; 26; 28; 30; 32; 34; 36; 38; 40 минут.

Измерения завершены, можно приступать к обработке результатов.