I.4. Решение систем линейных алгебраических уравнений методом обратной матрицы

Матрица, имеющая отличный от нуля определитель, называется невырожденной; имеющая равный нулю определитель – вырожденной.

Матрица 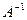называется обратной для заданной квадратной матрицы 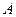, если при умножении матрицы 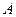на обратную ей как справа, так и слева, получается единичная матрица, то есть 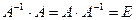. (1.7)

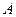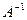Заметим, что в данном случае произведение матриц и коммутативно.

Теорема 1.2. Необходимым и достаточным условием существования обратной матрицы для заданной квадратной матрицы, является отличие от нуля определителя заданной матрицы

Если главная матрица системы оказалась при проверке вырожденной, то для нее не существует обратной, и рассматриваемый метод применить нельзя.

Для невырожденной матрицы 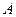можно найти обратную ей матрицу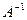

по следующему алгоритму.

1. Транспонируем матрицу 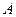в матрицу .

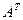2. Вычисляем алгебраические дополнения 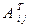элементов матрицы 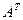и записываем их в матрицу .

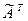3. Составим обратную матрицу 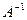по формуле:

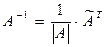. (1.8)

4. Сделаем проверку правильности найденной матрицы А^-1 согласно формуле (1.7). Заметим, что данная проверка может быть включена в итоговую проверку самого решения системы.

Система (1.5) линейных алгебраических уравнений может быть представлена в виде матричного уравнения: 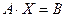, где 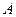– главная матрица системы, 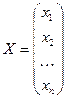– столбец неизвестных, 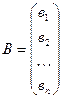– столбец свободных членов. Умножим это уравнение слева на обратную матрицу 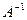, получим:

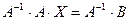. Так как по определению обратной матрицы 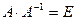, то уравнение принимает вид 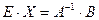или 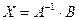. (1.9)

Таким образом, чтобы решить систему линейных алгебраических уравненийнужно столбец свободных членов умножить слева на матрицу, обратную для главной матрицы системы. После этого следует сделать проверку полученного решения.

Пример 1.6. Решить систему методом обратной матрицы

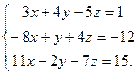
Решение. Вычислим главный определитель системы

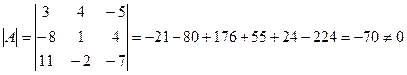. Следовательно, матрица 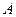невырожденная и обратная к ней матрица существует.

Найдём алгебраические дополнения всех элементов главной матрицы :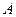

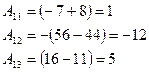
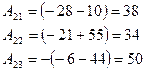
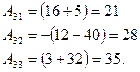
Запишем алгебраические дополнения в матрицу

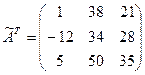. Воспользуемся формулами (1.8) и (1.9) для нахождения решения системы

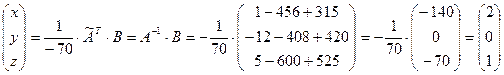. Отсюда

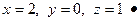
Вопросы для самопроверки.

1. Какая матрица называется вырожденной, невырожденной?

2. Какая матрица называется обратной для заданной? Каково условие ее существования?

3. Каков алгоритм нахождения обратной матрицы для заданной?

4. Какому матричному уравнению эквивалентна система линейных алгебраических уравнений?

5. Как решить систему линейных алгебраических уравнений с помощью обратной матрицы для главной матрицы системы?