Наружной СТЕНЫ МЕТОДОМ ЭЛЕКТРИЧЕСКОГО МОДЕЛИРОВАНИЯ

Цель работы: изучение и построение одномерного температурного поля наружной стены в условиях стационарной теплопередачи; расчеты тепловых потоков, термического сопротивления.

Оборудование: установка - электрическая модель фрагмента наружной стены из сплошной кирпичной кладки.

1.1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ [1]

В наружных ограждениях за счет разности температур внутреннего и наружного воздуха возникает передача тепла, направленная в сторону понижения температуры. Передача тепла в общем случае может осуществляться теплопроводностью, конвекцией и излучением. Передача тепла через однородное тело осуществляется в основном теплопроводностью. Процесс теплопроводности описывается дифференциальным уравнением Фурье:

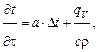(1.1)

где t - температура; τ - время; a - коэффициент температуропроводности; 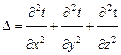- оператор Лапласа; с – удельная теплоемкость среды; 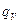– объемная мощность внутренних источников тепла; ρ – плотность среды.

Если процесс передачи тепла является стационарным ( 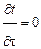) и внутренние источники тепла отсутствуют (q_v = 0), то уравнение (1.1) упрощается и преобразуется к уравнению Лапласа, которое в декартовой системе координат имеет вид:

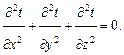(1.2)

Электрическое моделирование тепловых процессов основано на математическом подобии уравнений электро- и теплопроводности. Несмотря на различие физической природы этих явлений, они описываются одинаковыми по форме уравнениями. В частности, для электростатического поля в вакууме справедливо такое же уравнение Лапласа, что и уравнение (1.2), но вместо температуры t в нем фигурирует потенциал электрического поля U:

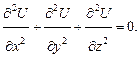(1.3)

В связи с этим для определения тепловых характеристик ограждающих конструкций задачу непосредственного измерения тепловых характеристик в натуре можно свести к задаче измерения электрических параметров в модели.

При создании электрической модели конкретной ограждающей конструкции необходимо учитывать количественные соотношения между тепло- и электропроводностью, которые следуют из аналогии законов Фурье и Ома в дифференциальной (локальной) форме:

,

.

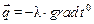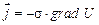где 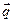- вектор плотности теплового потока; 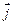- вектор плотности электрического тока; λ, σ - коэффициенты теплопроводности и электропроводности.

Таким образом, в методе электрического моделирования должны выполняться три основных принципа подобия натуры и модели:

1. Геометрическое подобие формы. Этот принцип означает, что расстояния между любыми сходными точками на модели и в натуре должны быть пропорциональны друг другу (коэффициент подобия - ).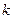

2. Сходство математических уравнений.

3. Подобие физических констант. Это подобие означает, что коэффициенты тепло- и электропроводности в сходных точках должны изменяться пропорционально друг другу:

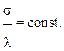
В соответствии с изложенными принципами создается модель, например плоской наружной стены, из листа электропроводной бумаги, которому придается форма, подобная форме исследуемой конструкции. Если толщина конструкции значительно меньше остальных ее размеров, то можно считать, что тепловой поток распространяется только в одном направлении: перпендикулярно поверхности стены. В этом случае можно использовать по аналогии законы Фурье и Ома в интегральном форме:

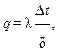(1.3)

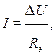(1.4)

где q - плотность теплового потока тепла через единицу поверхности стены; Δt - разность температур на поверхностях плоского слоя; δ - толщина плоского слоя; I - величина тока; R_э – электрическое сопротивление проводника, на концах которого поддерживается разность потенциалов ΔU.

Сравнение уравнений (1.3) и (1.4) позволяет установить аналогию между плотностью теплового потока q и величиной тока I; между перепадом температур Δt и разностью потенциалов ΔU, между коэффициентами λ и σ, а также позволяет ввести понятие теплового сопротивления R_т, аналогично понятию электрического сопротивления:

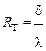
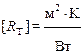(не Омы!).

Модуль плотности теплового потока вычисляется по формуле:

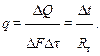
Термическим сопротивлением однослойной конструкции R_тназывается величина:

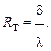
Таким образом:

; .

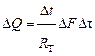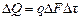Малоподвижные слои воздуха, находящиеся непосредственно у поверхностей конструкций, также обладают термическими сопротивлениями. В связи с этим для внутренней поверхности можно ввести понятие сопротивления тепловосприятию R_в, а для наружной - сопротивление теплоотдаче R_н. Величины этих сопротивлений

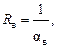
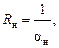
где α_в – коэффициент тепловосприятия внутренней поверхности; α_н – коэффициент теплоотдачи наружной поверхности.

Численные значения α_в и α_н приводятся в СНиПе.

Общее термическое сопротивление ограждающей конструкции определяется по формуле:

.

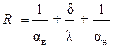В стационарных условиях плотность теплового потока, проходящего любую плоскость сечения ограждающей конструкции, имеет постоянную величину, что позволяет записать следующие соотношения:

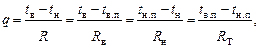(1.5)

где t_в, t_н, t_н.п и t_в.п – температура внутреннего, наружного воздуха, наружной и внутренней поверхностей соответственно.

Решая уравнения (1.5) относительно t_в.п, получим формулу для определения температуры внутренней поверхности конструкций:

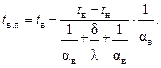
Температура воздуха внутри помещения 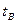отлична от температуры стены t_в.п (скачок температур).

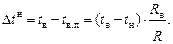
Значение Δt^н (скачка температуры) нормируется в СНиП.

Аналогично можно вычислить температуру в любой плоскости конструкции, зная термическое сопротивление между этой поверхностью и поверхностью наружной стены.

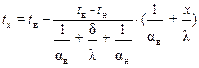
Из метеорологических наблюдений в каждой местности задают значения t_н. В строительном деле используют усредненные данные за период ≥10 лет. Для Вологодской области и Череповца величины среднемесячных по году температур t_н приведены в таблице (см. Приложение, табл. 5. Там же приведены значения 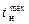и 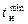, <t>).

Значение температур t_в важно для нормального функционирования человека в помещении. Оптимальная температура для работы умственного характера 23-24 °С. Температура 27-28 °С воспринимается как жарко, 17-18 °С – прохладно, 14-12 °С – холодно. При задании значения t_в руководствуются данными Приложения, табл. 6.

При физиологической приемлемости помещения важной вехой является температура t_в.п, перепад температур Δt^н = t_в – t_в.п и относительная влажность f %. Значения температур t_в, t_в.п, Δt^н влажности нормируются в СНиП, причем должно быть обязательно t_в.п > t_d, где t_d – точка росы [1, с. 45-46].

1.2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

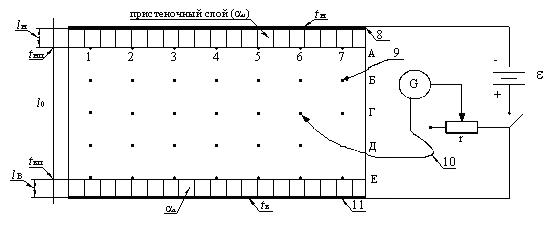
На рис. 1.1 приведена схема установки к лабораторной работе 1.

Рис. 1.1. Электрическая модель фрагмента плоской стены

Экспериментальные установки лабораторных работ 1, 2, и 3 представляют собой электрические модели конкретных ограждающих конструкций: наружной стены, наружного угла и стены с теплопроводным включением. Эти модели изготовлены из электропроводного материала (графитизированной бумаги).

Принципы создания экспериментальной модели (стены, угла):

- выбирается лист электропроводной бумаги, такой чтобы дли на листа была бы много больше его ширины;

- пусть ширина листа модели l_м (рис.1.2), на листе следует выделить три полоски: две – моделирующие пристеночные слои (, l_в), одну - моделирующую стену (l₀).

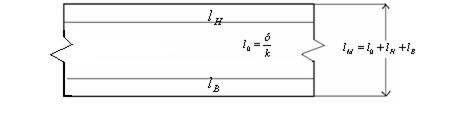
Рис. 1.2. К расчету ширины полосок l_н и l_в

Значения l₀, l_в, l_н определяют с соблюдением масштаба сопротивлений из соотношений:

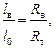где ;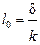

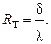
Откуда следует: 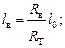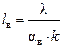и аналогично .

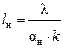В электрической модели лабораторного практикума по строительной физике надо оговорить одну особенность. Для каждого конкретного значения параметров α_в, α_н, λ и k (коэффициент подобия) необходимо изменять ширину полосок l_н и l_в, что очень непросто сделать в учебной лаборатории. Студентам выдаются индивидуальные различные значения λ и k, что может привести к «краевым эффектам» нарушающим точное соответствие «строительная конструкция – модель». Особенно важно это при расчетах тепловых потоков и температурных скачков на границах.

Температуру окружающей среды моделируют электрические потенциалы, подаваемые на шины 8 и 11 через выключатель К (см. рис. 1.1) от источника постоянного тока ε.

Одна клемма выключателя К через переменный резистор r и гальванометр G соединена со свободным щупом 10. Величина переменного резистора r подобрана так, чтобы ток щупа был значительно меньше общего тока, проходящего через модель. Выполнение этого условия необходимо для того, чтобы ток щупа не искажал электрическое поле модели. В этом случае ток, измеренный гальванометром, будет пропорционален потенциалу точки квазистатического поля, к которой прикасается щуп. Все поле модели разбито сеткой, в узлах которой установлены клеммы 9. Наличие оси симметрии позволяет усреднять результаты измерений (конечно, если в модели нет дефектов).

1.3. ПОРЯДОК ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

При проведении опытов необходимо выполнить указание (пункт 5) по технике безопасности.

Измерения проводятся следующим образом.

1. После того как обеспечен надежный контакт щупа с шиной, имитирующей температуру наружного воздуха, необходимо включить выключатель К и, регулируя величину сопротивления r, вывести стрелку гальванометра на максимальное деление n_max (задать температурный масштаб (t_в – t_н ~ n_max).

Касаясь щупом поочерёдно каждой клеммы, измерить и записать в таблицу по форме 1 ток щупа I в делениях шкалы гальванометра n_i.

Форма 1

1.4. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

1. Величины, задаваемые преподавателем: температура внутреннего t_в и наружного t_н воздуха, коэффициенты теплопроводности λ, тепловосприятия α_в, теплоотдачи α_н и коэффициент подобия k, относительная влажность воздуха в помещении f₁ %, f₂ % (сухо, нормально, повышенная).

2. При выполнении принципов аналогии между моделью и натурой справедливо соотношение:

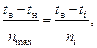
из которого следует расчетная формула для температуры t_i определенной точки конструкции:

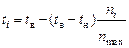(1.6) ,

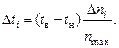
По формуле (1.6) следует рассчитать для плоскостей А, Б, Г, Д и Е значения температуры по усредненным показаниям гальванометра n_i.

3. Вычертить на миллиметровой бумаге (в масштабе) кривую изменения температуры по толщине реальной (не модели!) стены δ. Примерный вид этой кривой показан на рис. 1.3.

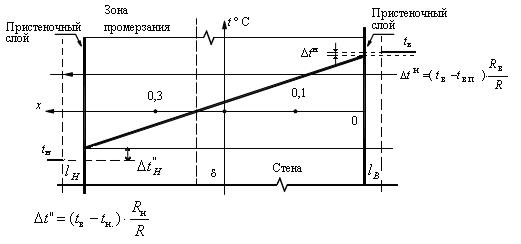
Рис. 1.3. Распределение температуры по толщине конструкции

4. По графику определить глубину промерзания стены (зону отрицательных температур), отсчитанную от внутренней поверхности.

5. По заданному значению t_в и относительной влажности воздуха в помещении найти точку росы t_d [1, c. 45-46] и сравнить ее с температурой внутренней поверхности стены t_в.п (плоскость Е на модели). Дать заключение о возможности выпадения конденсата на этой поверхности.

6. Определить плотность теплового потока q, проходящего через стену (удельную потерю тепла), по формуле Ньютона:
q^N = α_в(t_в – t_в.п) = α_н (t_н.п – t_н), и по формуле Фурье: 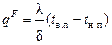. Сравнить их.

7. Рассчитать величину термических сопротивлений ; .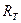

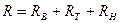8. Определить, при какой максимальной температуре наружного воздуха на внутренней поверхности стены начнется выпадение конденсата при q = const.

Контрольные вопросы

1. Проведите аналогию между температурным и электрическим полями на основе дифференциальных уравнений, соответствующих законам Ома и Фурье.

2. Что такое коэффициент теплопроводности, коэффициент тепловосприятия, коэффициент теплоотдачи? Запишите единицы измерения этих величин.

3. Каков физический смысл величин, указанных в предыдущем пункте?

4. От чего зависит коэффициент теплопроводности строительных материалов?

5. Приведите границы для интервала значений коэффициента теплопроводности строительных материалов. Назовите некоторые из них с указанием числа λ (см. Приложения, табл. 1).

Литература

1. Федорчук Н.М., Грызлов В.С. Избранные главы физики в строительном деле: Учеб. пособие. – Череповец, 1994.

2. СНиП РФ 23-02-2003 «Тепловая защита зданий»; СП 23-101-2004 «Проектирование тепловой защиты зданий».

3. СНиП 23-01-99 «Строительная климатология». СНиП 2.01.01-82 «Строительная климатология и геофизика».