Алгоритмы линейной структуры

Линейные алгоритмы предполагают последовательное выполнение действий в порядке, заданном схемой, без их повторения или пропуска некоторых действий. Алгоритм линейной структуры изображается линейной последовательностью связанных друг с другом блоков (рис. 9.8). Такой порядок выполнения действий называется естественным. Поэтому в схемах алгоритмов линейной структуры нет блока «Решение».

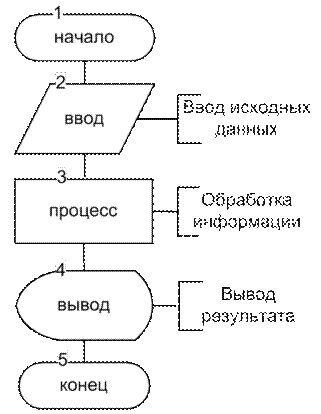
Рис. 9.8. Алгоритм линейной структуры

В тестовом задании ниже представлен линейный вычислительный процесс. Фрагмент данного алгоритма записан в словесно-формульном виде.

Тестовое задание 9.7.

Чему равны значения переменных а и b после выполнения следующего фрагмента алгоритма:

1) а = 3;

2) b = 7;

3) b = a;

4) a = b;

5) b = b*2

Ответы:

6) a = 3; b = 6

7) a = 14; b = 7

8) a = 7; b = 14

9) a = 6; b = 3

10) a = 3; b = 14

Решение. Выполняем алгоритм последовательно по шагам:

1) а = 3;

2) b = 7;

3) b = a; знак равенства «=» в этом случае трактуется как знак присваивания «=:», следовательно, переменной b присваивается значение переменной а=3; т.е. переменная b примет значение b=3;

4) a=b; переменной а присваивается значение переменной b=3; следовательно, переменная а примет значение а =3;

5) b=b*2; переменной b присваивается значение b*2 (к этому моментупеременная b имеет значение b=3); следовательно, переменная b примет значение b= b·2=3·2=6.

Таким образом, в результате выполнения алгоритма переменные а и b примут значения a = 3; b = 6.

Визуальное представление данного фрагмента алгоритма в виде блок-схемы представлено на рисунке 9.9.

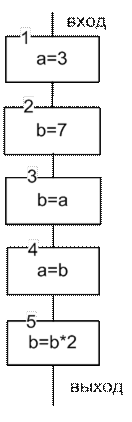
Рис. 9.9. Визуальное представление фрагмента линейного алгоритма