Векторы на плоскости и в пространстве.
Тема 3. Векторные пространства
Векторы на плоскости и в пространстве.
Вектором называется направленный отрезок 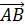 с начальной точкой
с начальной точкой 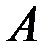 и конечной точкой
и конечной точкой 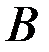 (рис. 3.1). Векторы могут обозначаться как двумя прописными буквами, так и одной строчной со стрелкой, например:
(рис. 3.1). Векторы могут обозначаться как двумя прописными буквами, так и одной строчной со стрелкой, например: 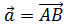 .
.
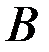
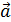
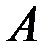
Рис. 3.1
Длиной (или модулем) 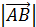 вектора
вектора 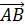 называется число, равное длине отрезка
называется число, равное длине отрезка 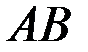 , изображающего вектор.
, изображающего вектор.
Если начало и конец вектора совпадают, например, 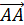 , то такой вектор называется нулевым и обозначают
, то такой вектор называется нулевым и обозначают 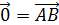 .
.
Длина нулевого вектора равна нулю 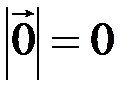 .
.
Произведением вектора  на число
на число 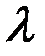 называется вектор
называется вектор 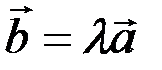 , имеющий длину
, имеющий длину 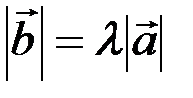 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора  , если
, если 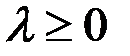 , и противоположно ему, если
, и противоположно ему, если 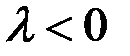
Противоположным вектором 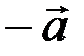 называется произведение вектора на число
называется произведение вектора на число 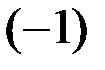 , т.е.
, т.е. 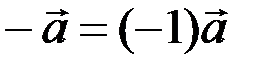 .
.
Суммой двух векторов  и
и 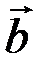 называется вектор
называется вектор 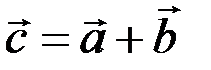 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец - с концом вектора
, а конец - с концом вектора 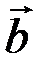 при условии, что начало вектора вектора
при условии, что начало вектора вектора  совпадает с концом вектора
совпадает с концом вектора  (правило треугольника).
(правило треугольника).
Очевидно, что вектор 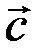 представляет диагональ параллелограмма, построенного на векторах
представляет диагональ параллелограмма, построенного на векторах  и
и 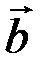 (рис. 3.2).
(рис. 3.2).
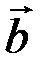

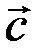
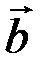
Рис. 3.2.
Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов  ,
, 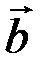 ,
, 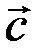 и
и 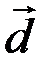 есть вектор
есть вектор 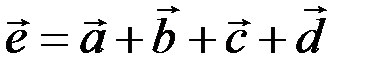 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец - с концом вектора
, а конец - с концом вектора 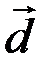 (рис. 3.3).
(рис. 3.3).
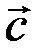
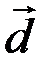

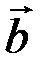
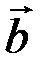
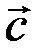

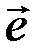
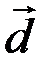
Рис. 3.3.
Нетрудно убедиться, что вектор 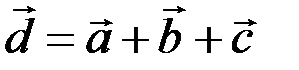 , определяемый таким образом, представляет собой диагональ параллелепипеда, построенного на векторах
, определяемый таким образом, представляет собой диагональ параллелепипеда, построенного на векторах  ,
, 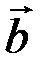 и
и 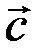 , не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда).
, не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда).
Разностью двух векторов  и
и 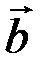 называется сумма вектора
называется сумма вектора  и вектора
и вектора 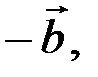 противоположного вектору
противоположного вектору 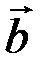 (рис 3.4).
(рис 3.4).
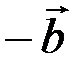

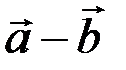

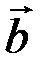
Рис. 3.4.
Легко убедиться, что в параллелограмме, построенном на векторах 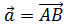 и
и 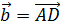 , одна диагональ - вектор
, одна диагональ - вектор 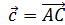 - представляет сумму векторов
- представляет сумму векторов  и
и 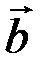 , а другая диагональ - вектор
, а другая диагональ - вектор 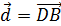 - их разность (рис. 3.5).
- их разность (рис. 3.5).
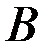
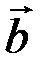

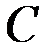

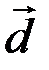
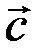
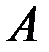
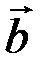
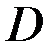
Рис. 3.5.
Перенесем вектор  параллельно самому себе так, чтобы его начало совпало с началом координат.
параллельно самому себе так, чтобы его начало совпало с началом координат.
Координатами вектора  называются координаты его конечной точки. Так, координатами вектора
называются координаты его конечной точки. Так, координатами вектора 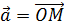 на плоскости
на плоскости 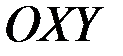 являются два числа
являются два числа 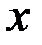 и
и 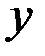 (
( 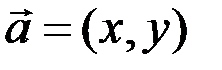 - рис. 3.6), а в пространстве
- рис. 3.6), а в пространстве 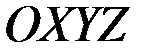 - три числа
- три числа 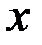 ,
, 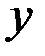 и
и 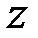 (
( 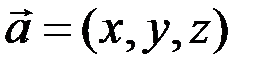 - рис. 3.7).
- рис. 3.7).
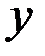
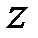
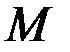
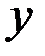
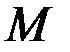
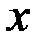

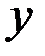

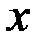
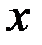
Рис. 3.6. Рис. 3.7.
В соответствии с определениями, приведенными выше, нетрудно показать, что суммой и разностью векторов 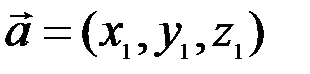 и
и 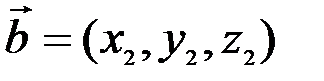 являются векторы
являются векторы
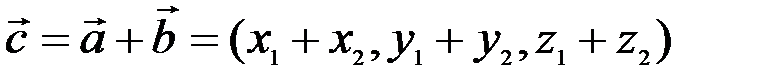 ,
,
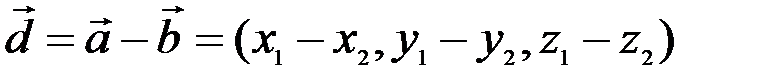 ,
,
А произведение вектора 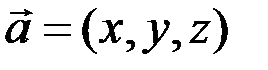 на число
на число 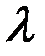 есть вектор
есть вектор 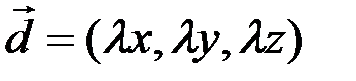 .
.
На рис. 3.6 и 3.7 видно, что длина вектора равна корню квадратному из суммы квадратов его координат:
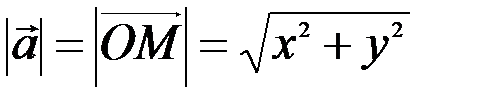
или
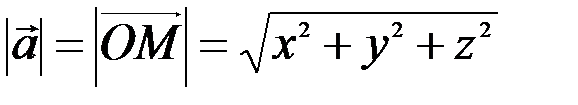 . (3.1)
. (3.1)
Если вектор 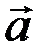 составляет угол
составляет угол 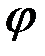 с осью
с осью 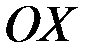 , то проекцией вектора на эту ось называется произведение модуля вектора на косинус угла
, то проекцией вектора на эту ось называется произведение модуля вектора на косинус угла 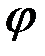
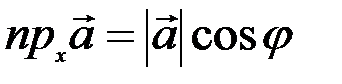 .
.
Проекция суммы векторов  и
и 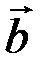 на ось
на ось 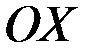 равна сумме проекций этих векторов на эту ось
равна сумме проекций этих векторов на эту ось
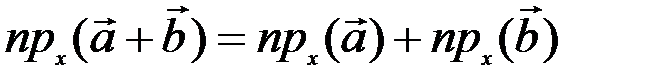 .
.
Косинусы углов 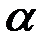 ,
, 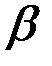 ,
, 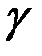 , образованных вектором
, образованных вектором  с осями координат, находятся в виде отношений
с осями координат, находятся в виде отношений

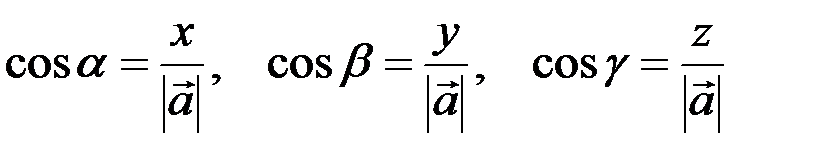 .
.
и называются направляющими косинусами.
Равенство 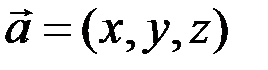 используется для выражения вектора
используется для выражения вектора 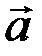 через его проекции на заданные координатные оси.
через его проекции на заданные координатные оси.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Условие коллинеарности двух векторов 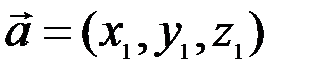 и
и 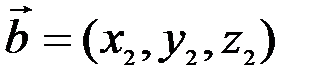 записывается в виде
записывается в виде
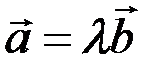
где 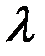 - числовой множитель. Через координаты это условие записывается в виде
- числовой множитель. Через координаты это условие записывается в виде
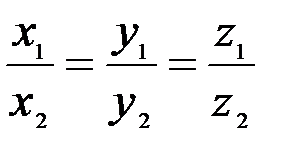 .
.
Очевидно, что нулевой вектор коллинеарен любому вектору.
Векторы, параллельные одной плоскости, называются компланарными.
Скалярным произведением 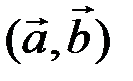 двух векторов
двух векторов 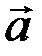 и
и 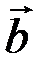 называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 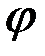 между ними:
между ними:
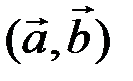 =
= 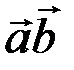 =
= 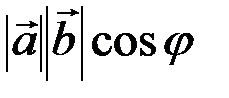 .
.
Выразим скалярное произведение через координаты векторов 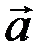 и
и 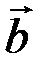 . Из треугольника
. Из треугольника 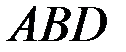 (рис. 3.5), сторонами которого являются
(рис. 3.5), сторонами которого являются 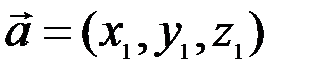 ,
, 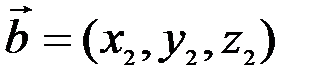 и
и 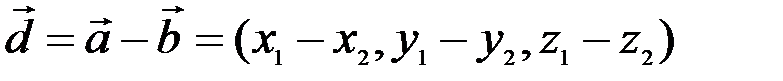 , по теореме косинусов следует, что
, по теореме косинусов следует, что
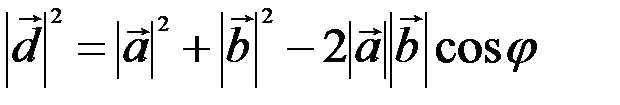 ,
,
откуда
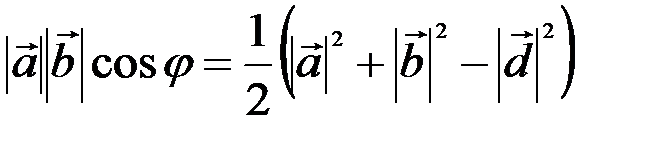 , (3.2)
, (3.2)
Так как по формуле (3.1) длины векторов 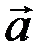 ,
, 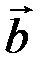 и
и 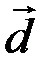 равны соответственно
равны соответственно
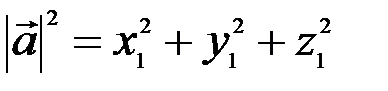 ,
,
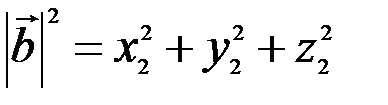 ,
,
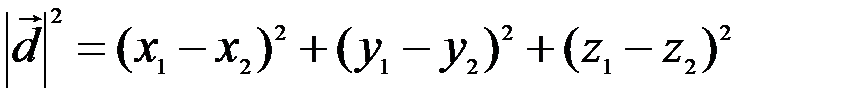 ,
,
после преобразования выражения (3.2) получим
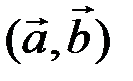 =
= 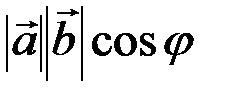 =
= 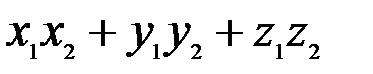 , (3.3)
, (3.3) 
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Векторы 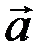 и
и 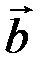 называются ортогональными, если их скалярное произведение равно нулю
называются ортогональными, если их скалярное произведение равно нулю
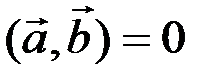 или
или 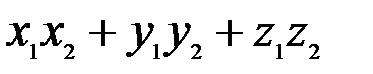 =0
=0
Скалярное произведение обладает следующими свойствами:
1) 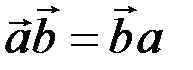 ;
;
2) 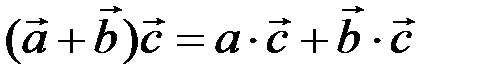 .
.
Заметим, что при 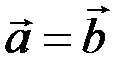 угол
угол 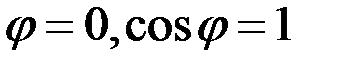 и
и
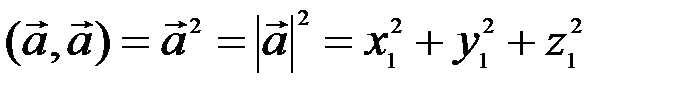 . (3.4)
. (3.4)
т.е. скалярный квадрат вектора равен квадрату его длины. В частности, расстояние 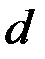 между двумя точками плоскости
между двумя точками плоскости 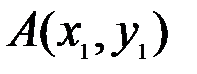 и
и 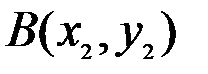 можно рассматривать как длину вектора
можно рассматривать как длину вектора 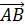
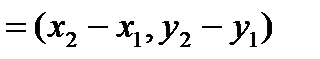 . Поэтому
. Поэтому
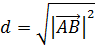 =
= 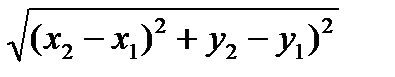 . (3.5)
. (3.5)
Угол между векторами 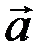 и
и 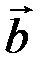 определяется по формуле
определяется по формуле
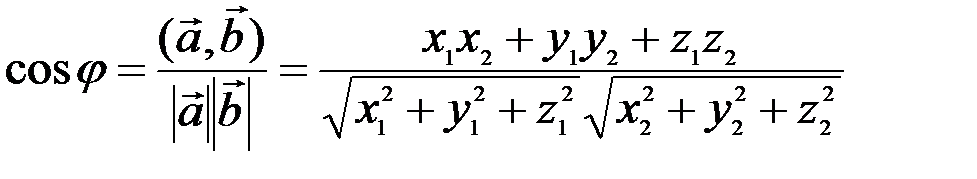 (3.6)
(3.6)
Пример 3.1. Даны векторы 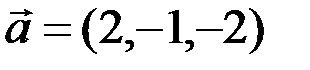 и
и 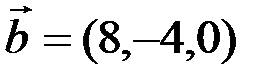 . Найти векторы
. Найти векторы 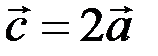 ,
, 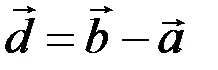 и длины векторов
и длины векторов 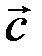 и
и 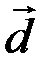 .
.
Решение. По определению 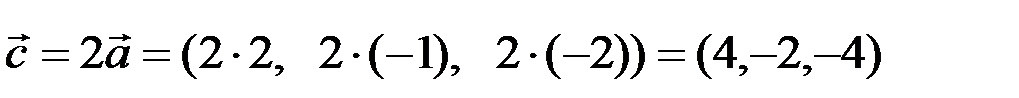 ,
, 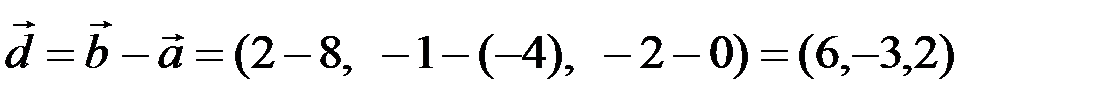 .
.
По формуле (3.1) найдем длины векторов 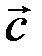 и
и 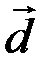
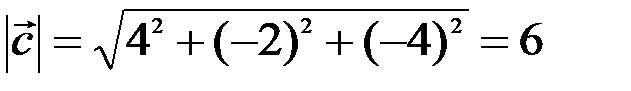 ,
, 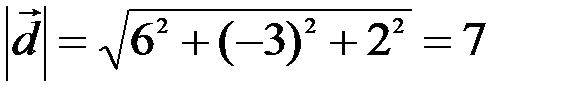
Пример 3.2.Для векторов 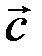 и
и 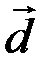 из примера 3.1 найти скалярный квадрат вектора
из примера 3.1 найти скалярный квадрат вектора 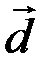 , скалярное произведение векторов
, скалярное произведение векторов 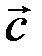 и
и 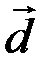 и угол между ними.
и угол между ними.
Решение. По формуле (3.4) скалярный квадрат равен квадрату модуля вектора, т.е.
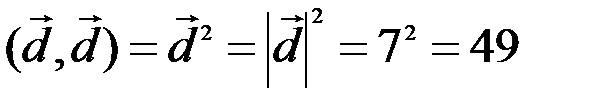 .
.
По формуле (3.3) для скалярного произведения векторов 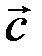 и
и 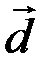 имеем
имеем
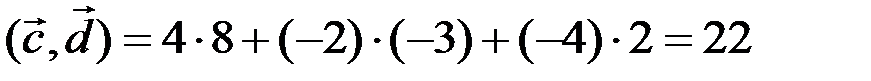 .
.
По формуле (3.6) угол между векторами 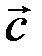 и
и 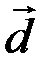 определяется равенством
определяется равенством
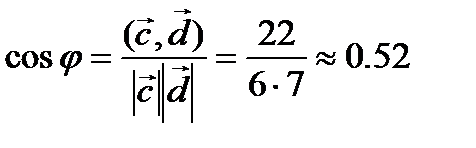 ,
,
откуда 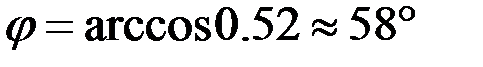 .
.
Пример 3.3. Даны два вектора 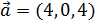 и
и 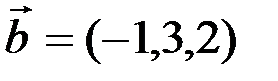 . Вычислить скалярное произведение двух векторов
. Вычислить скалярное произведение двух векторов 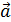 и
и 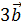 . Проверить, будут ли коллинеарны или ортогональны два вектора
. Проверить, будут ли коллинеарны или ортогональны два вектора 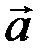 и
и 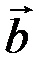 .
.
Решение. Найдем скалярное произведение
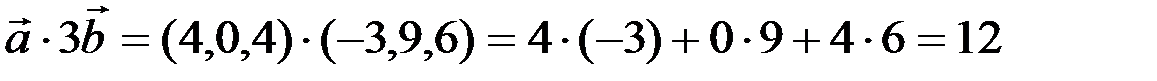
Проверим выполнение условия коллинеарности, т.е. 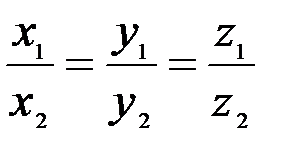 . Т.к.
. Т.к. 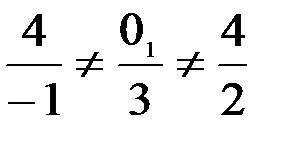 , то векторы
, то векторы 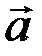 и
и 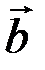 не коллинеарны.
не коллинеарны.
Проверим выполнение условия ортогональности, т.е. 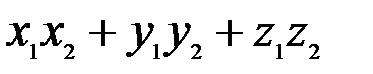 =0. Поскольку
=0. Поскольку 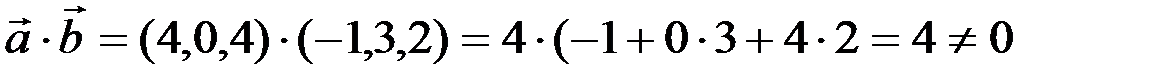 , то векторы
, то векторы 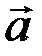 и
и 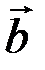 не ортогональны.
не ортогональны.
Тройка некомпланарных векторов векторов  ,
, 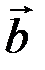 и
и 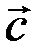 называется правой, если наблюдателю из их общего начала обход концов векторов
называется правой, если наблюдателю из их общего начала обход концов векторов 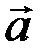 ,
,  ,
, 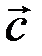 в указанном порядке кажется совершающимся по часовой стрелке. B противном случае
в указанном порядке кажется совершающимся по часовой стрелке. B противном случае 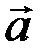 ,
,  ,
, 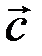 - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
- левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
Тройка 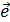 1,
1, 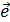 2,
2, 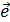 3 некомпланарных векторов вR3 называется базисом, а сами векторы
3 некомпланарных векторов вR3 называется базисом, а сами векторы 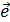 1,
1, 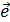 2,
2, 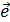 3 - базисными. Любой вектор
3 - базисными. Любой вектор 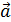 может быть единственным образом разложен по базисным векторам, то есть представлен в виде
может быть единственным образом разложен по базисным векторам, то есть представлен в виде
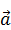 = x1
= x1 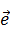 1 + x2
1 + x2 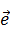 2+x3
2+x3 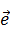 3,
3,
Числа x1, x2, x3 в соответствии с введенным выше определением являются координатами вектора 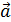 в базисе
в базисе 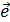 1,
1, 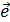 2,
2, 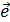 3. Если векторы
3. Если векторы 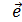 1,
1, 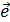 2,
2, 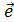 3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x1, x2, x3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать
3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x1, x2, x3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать 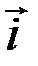 ,
,  ,
, 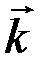 .
.
Будем предполагать, что в пространстве R3 выбрана правая система декартовых прямоугольных координат { 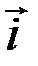 ,
,  ,
, 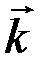 }.
}.
Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор 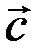 , который определяется следующими тремя условиями:
, который определяется следующими тремя условиями:
1. Длина вектора 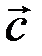 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах  и
и  ,т. е. ê
,т. е. ê 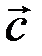 ê = ê
ê = ê  ê ê
ê ê  êsin (
êsin (  ^
^  ).
).
2. Вектор 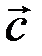 перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов  и
и 
3. Векторы  ,
,  и
и 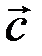 , взятые в указанном порядке, образуют правую тройку.
, взятые в указанном порядке, образуют правую тройку.
Для векторного произведения 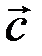 вводится обозначение
вводится обозначение 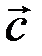 =
=  ´
´  (иногда векторное произведение обозначают
(иногда векторное произведение обозначают 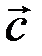 =[
=[ 
 ]).
]).
Если векторы  и
и  коллинеарны, то sin(
коллинеарны, то sin(  ^
^  ) = 0 и
) = 0 и 

 = 0. В частности,
= 0. В частности, 

 = 0, а векторные произведения ортов:
= 0, а векторные произведения ортов: 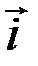

 =
= 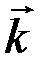 ,
, 

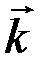 =
= 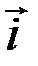 ,
, 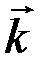

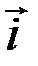 =
=  .
.
Если векторы  и
и  заданы координатами
заданы координатами  = (a1, a2, a3),
= (a1, a2, a3),  = (b1, b2, b3), то
= (b1, b2, b3), то


 =
= 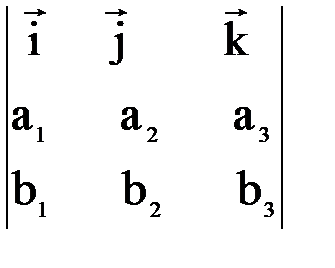
где выражение
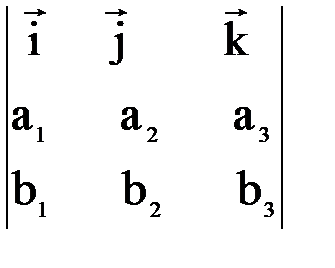 =
= 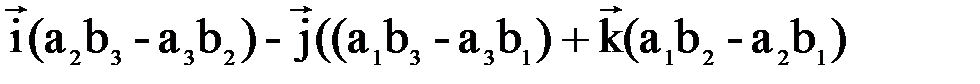
- определитель 3-его порядка.
Если векторное произведение двух векторов  и
и  скалярноумножается на третий вектор
скалярноумножается на третий вектор 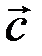 , то такое произведение трех векторов называется смешанным произведением
, то такое произведение трех векторов называется смешанным произведением
Если векторы  ,
,  и
и 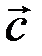 заданы своими координатами
заданы своими координатами
 =(a1, a2, a3),
=(a1, a2, a3),  =(b1, b2, b3),
=(b1, b2, b3), 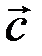 = (c1, c2, c3), то
= (c1, c2, c3), то
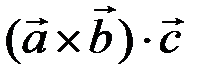 =
= 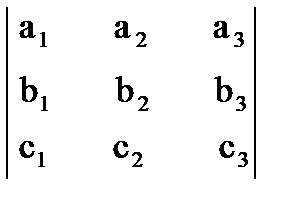 .
.
Отметим основные свойства смешанного произведения:
1. От перестановки двух любых сомножителей смешанное произведение меняет знак
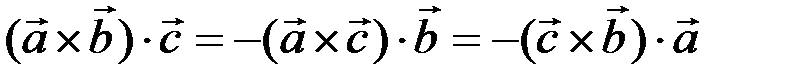
2. Если два из трех данных векторов равны или параллельны, то их смешанное произведение равно нулю.
3. Знаки операций "точка" и "крест" можно менять местами
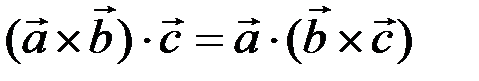
поэтому смешанное произведение принято записывать в виде 

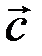 , т.е. без скобок и без знаков действий
, т.е. без скобок и без знаков действий
4. (Условие компланарности) Если три вектора 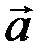 ,
, 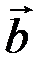 и
и 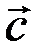 компланарны, то их смешанное произведение равно нулю
компланарны, то их смешанное произведение равно нулю
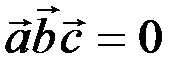 .
.
Верно и обратное утверждение.
Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.
Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка


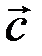 - левая, то
- левая, то 

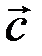 <0 и V = -
<0 и V = - 

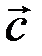 , следовательно V = ê
, следовательно V = ê 

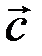 ê.
ê.
Пример 3.4. Зная векторы  и
и  , на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной к стороне a.
, на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной к стороне a.
Решение. Обозначим 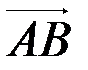 =
=  ,
, 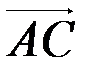 =
=  ,
, 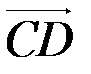 =
=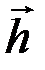 , где
, где 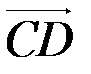 ^
^  , D - основание
, D - основание
C
 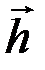 D
D 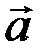 А B
А B
| перпендикуляра, опущенного из точки C на сторону 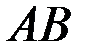 . По правилу сложения векторов имеем: . По правилу сложения векторов имеем:  + + 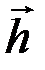 = = 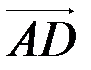 , , 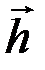 = = 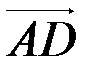 - -  .Поскольку .Поскольку 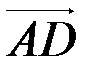 çç çç  , то , то 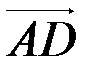 = l = l  .
Найдем значение l, используя ортогональность векторов .
Найдем значение l, используя ортогональность векторов  и и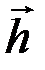 : :  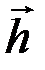 =0 или =0 или  (l (l  - -  )=0, откуда l = )=0, откуда l =   / /  2. Следовательно, 2. Следовательно, 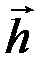 = ( = (   / /  2) 2)  - -  . .
|
Пример 3.5.Найти угол между векторами  = 2
= 2 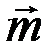 +4
+4 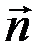 и
и  =
= 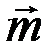 -
- 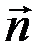 , где
, где 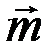 и
и 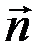 -единичные векторы и угол между
-единичные векторы и угол между 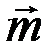 и
и 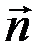 равен 120о.
равен 120о.
Решение. Имеем:
cos j = 
 /(|a||b|),
/(|a||b|),

 =(2
=(2 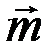 +4
+4 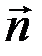 ) (
) ( 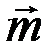 -
- 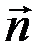 ) = 2
) = 2 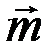 2 - 4
2 - 4 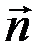 2 +2
2 +2 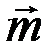
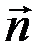 = 2 - 4+2cos120o = - 2 + 2(-0.5) = -3;
= 2 - 4+2cos120o = - 2 + 2(-0.5) = -3; 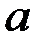 =
= 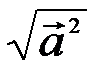 ;
;  2 = (2
2 = (2 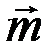 +4
+4 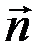 ) (2
) (2 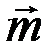 +4
+4 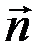 ) = 4
) = 4 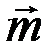 2 +16
2 +16 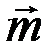
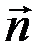 +16
+16 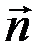 2 = 4+16(-0.5)+16=12, значит
2 = 4+16(-0.5)+16=12, значит 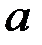 =
= 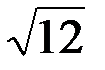 .
.
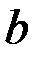 =
= 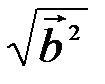 ;
;  2== (
2== ( 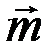 -
- 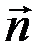 )(
)( 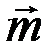 -
- 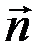 ) =
) = 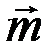 2 -2
2 -2 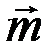
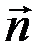 +
+ 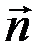 2 =1-2(-0.5)+1 = 3,
2 =1-2(-0.5)+1 = 3,
значит 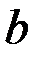 =
= 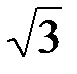 . Окончательно имеем: cos j =
. Окончательно имеем: cos j = 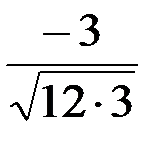 = -1/2, Þ j = 120o.
= -1/2, Þ j = 120o.
Пример 3.6.Зная векторы  =
= 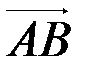 (-3,-2,6) и
(-3,-2,6) и  =
= 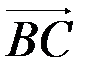 (-2,4,4),вычислите длину высоты AD треугольника ABC.
(-2,4,4),вычислите длину высоты AD треугольника ABC.
Решение. Обозначая площадь треугольника ABC через S, получим:
S = 1/2 BC AD.
Пусть 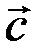 =
= 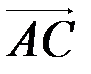 Тогда AD=2S/BC, BC=
Тогда AD=2S/BC, BC= 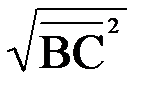 =
= 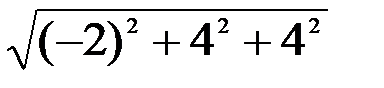 = 6,
= 6,
S = 1/2 ç  ´
´ 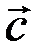 ç.
ç. 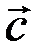 =
=  +
+  , значит, вектор
, значит, вектор 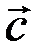 имеет координаты
имеет координаты
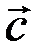 (-5,2,10).
(-5,2,10).  ´
´ 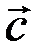 =
= 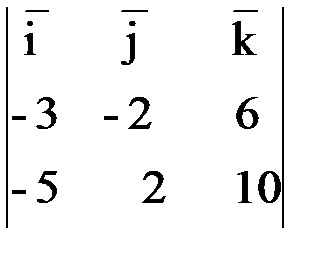 = i (-20 -12) - j (30 -30) + k (- 6 - 10) =
= i (-20 -12) - j (30 -30) + k (- 6 - 10) =
= -16(2`i +`k ). ç  ´
´ 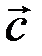 ç =
ç = 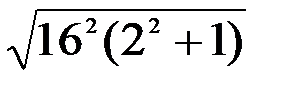 = 16
= 16 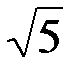 ; S = 8
; S = 8 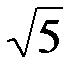 , откуда
, откуда
AD = 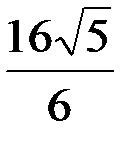 =
= 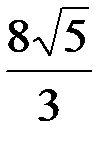 .
.
Пример 3.7. Даны два вектора  =(11,10,2) и
=(11,10,2) и  =(4,0,3). Найти единичный вектор
=(4,0,3). Найти единичный вектор 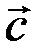 , ортогональный векторам
, ортогональный векторам  и
и  и направленный так, чтобы упорядоченная тройка векторов
и направленный так, чтобы упорядоченная тройка векторов  ,
,  ,
, 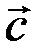 была правой.
была правой.
Решение. Обозначим координаты вектора 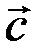 через x, y, z.
через x, y, z.
Поскольку 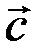 ^
^  ,
, 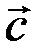 ^
^  , то
, то 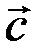
 = 0,
= 0, 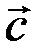
 = 0. По условию задачи требуется, чтобы
= 0. По условию задачи требуется, чтобы 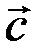 = 1 и
= 1 и 

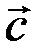 >0.
>0.
Имеем систему уравнений для нахождения x, y, z:
11x +10y + 2z = 0,
4x+3z=0,
x2 + y2 + z2 = 0.
Из первого и второго уравнений системы получим z = -4/3 x, y = -5/6 x. Подставляя y и z в третье уравнение, будем иметь: x2 = 36/125, откуда
x = ± 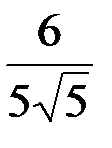 . Используя условие
. Используя условие 

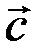 >0, получим неравенство
>0, получим неравенство
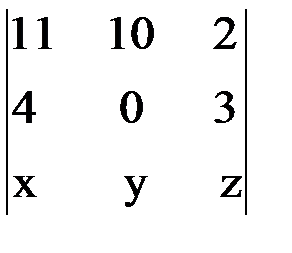 > 0 или 5(6x-5y-8z) > 0.
> 0 или 5(6x-5y-8z) > 0.
С учетом выражений для z и y перепишем полученное неравенство в виде: 625/6 x > 0, откуда следует, что x>0. Итак, x = 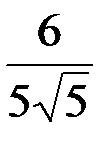 , y = -
, y = - 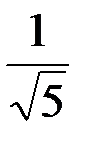 , z =-
, z =- 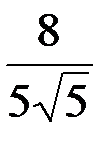 .
.
Дата добавления: 2015-09-29; просмотров: 2277;
