Cобственные значения и собственные векторы матриц
Тема 4. Cобственные значения и собственные векторы матриц. Квадратичные формы.
Cобственные значения и собственные векторы матриц
Число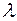 
называется собственным числом квадратной матрицы А, а ненулевой вектор 
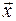- её собственным вектором, соответствующим числу 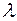, если выполняется равенство
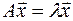(4.1) 
В равенстве (4.1) матрица А имеет порядок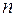 
, вектор 
, 
.
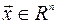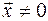Множество собственных чисел матрицы 
называется её спектром.
В литературе встречается и другая терминология: собственные числа иногда называют собственными значениями или характеристическими корнями, а собственные векторы - характеристическими векторами.
Матричное уравнение (4.1) можно переписать в виде
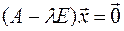(4.2)
где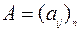 
, 
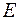- единичная матрица порядка n, 
, 
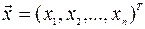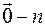-мерный нуль-вектор.
Матричное уравнение (4.2) представляет собой запись однородной системы линейных уравнений с переменными 
, 
, …, 
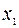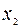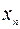. Матрица имеет собственный вектор 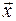, если существует нетривиальное решение этой системы. А поскольку система однородная, то нетривиальное решение существует тогда и только тогда, когда матрица системы (4.2) вырожденная, т.е. её определитель равен нулю
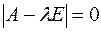(4.3)
Равенство (4.3) является уравнением n-ой степени относительно 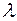. Действительно, оно имеет вид
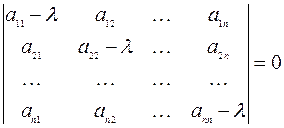
но в определителе n-ого порядка есть член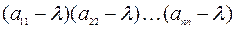 
с 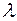в n-й степени. Во всех остальных членах определителя степень множителя 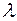меньше.
Уравнение (4.3) называется характеристическим уравнением матрицы A, а определитель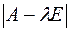 
- её характеристическим многочленом.
Итак, чтобы найти собственные числа матрицы, надо составить и решить её характеристическое уравнение.
Можно доказать, что алгебраическое уравнение n-й степени имеет n комплексных корней; часть корней или все эти корни могут быть вещественными. Среди вещественных корней могут быть и равные (кратные). Если уравнение (4.3) имеет мнимый корень, то оно имеет и сопряженный ему корень, так как все коэффициенты уравнения (4.3) - вещественные числа.
Пример 4.1.Найти собственные числа матрицы A
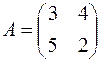
Решение. Составим и решим характеристическое уравнение матрицы A
, 
;
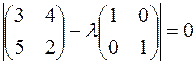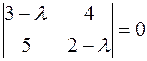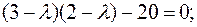
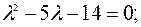
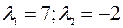
Итак, матрица A имеет вещественные собственные числа 7 и -2.
Следующая теорема (приводится без доказательства) устанавливает важное свойство характеристического многочлена квадратной матрицы.
Теорема 4.1 ( теорема Гамильтона-Кэли)
Если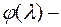 
характеристический многочлен A, то 
.
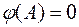Проверим это утверждение на примере.
Пример 4.2. Вычислить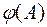 
для матрицы A из примера 4.1.
Решение. В уравнении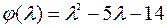 
подставим вместо 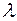матрицу А, умножив свободный член (-14) на единичную матрицу:
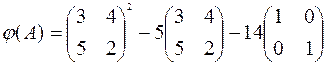
Вычислим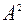 
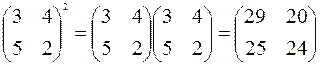
Тогда
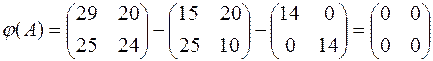
Для того чтобы найти собственный вектор, соответствующий собственному числу 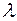, надо решить матричное уравнение (4.2), т.е. систему однородных линейных уравнений, матрица которой - вырожденная. Такая система имеет бесконечное множество решений.
Пример 4.3.Найти собственные векторы матрицы A из примера 4.1.
Решение. Собственные векторы матрицы А, соответствующие собственному числу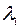 
=7, находим, решая систему
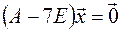
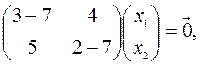
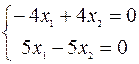
Эта система равносильна одному уравнению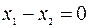 
, или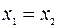 
. Собственными векторами матрицы А, соответствующими собственному числу 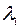=7, являются векторы 
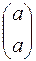, где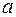 
- любое не равное нулю число. Собственные векторы матрицы А, соответствующие собственному числу 
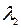=-2, находим, решая систему
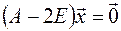
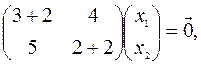
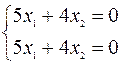
Эта система равносильна одному уравнению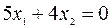 
, или
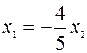
Собственными векторами матрицы А, соответствующими собственному числу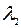 
=-2, являются векторы 
, 
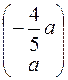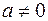или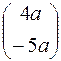 
, .
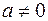Дата добавления: 2015-09-29; просмотров: 3487;