Симметрические матрицы и квадратичные формы

Симметрической называется квадратная матрица 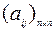, все элементы которой 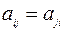при всех значениях 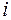и .

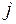Рассмотрим свойства симметрической матрицы.

1.

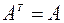
Это свойство непосредственно вытекает из определения симметрической матрицы.

2.Все собственные числа вещественной симметрической матрицы вещественны.

Проверим это свойство на матрице второго порядка.

Пусть 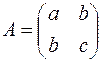. Составим характеристическое уравнение этой матрицы

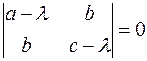
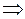
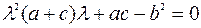
Найдем дискриминант полученного квадратного уравнения

.

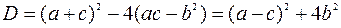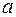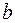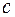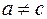Так как дискриминант неотрицателен при всех значениях , и , то уравнение имеет два вещественных корня, являющихся собственными числами матрицы . Если или 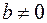, то матрица имеет два различных собственных числа. Есл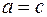и и 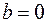, то матрица имеет два равных собственных числа. .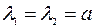

3.Собственные векторы вещественной симметрической матрицы, соответствующие различным собственным числам, ортогональны.

Пример 4.8. Найти собственные числа и собственные векторы симметрической матрицы

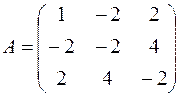
и показать, что собственные векторы этой матрицы, соответствующие различным собственным числам, ортогональны.

Решение. Составим и решим характеристическое уравнение матрицы

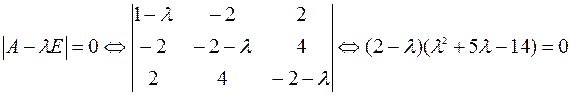
Собственными числами матрицы являются корни полученного характеристического уравнения

.

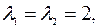
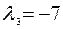Собственные векторы, соответствующие собственному числу 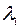и собственному числу 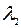, найдем, решив однородную систему линейных уравнений

.

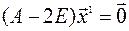
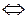
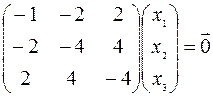
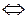
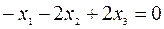Поскольку ранг системы равен 1, а число переменных -3, то две переменные, например, 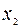и 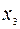, будут свободными и могут принимать произвольные значения, не равные нулю, 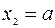и 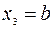, 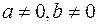. Тогда переменная 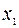примет значение 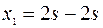, и собственные векторы будут иметь вид

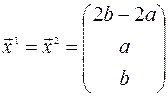
Собственный вектор матрицы , соответствующий собственному числу 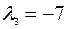, найдем, решив однородную систему линейных уравнений

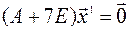
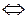
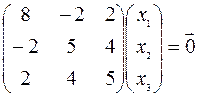
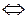
Выпишем матрицу системы и решим ее методом Гаусса. К 3-ей строке прибавим 2-ую, а затем вторую разделим на (-2) и поменяем местами с 1-ой. Получим

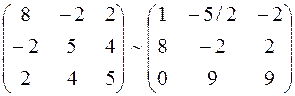
Затем разделим 2-ую строку на (-2) и сложим с 1-ой, умноженной на 4

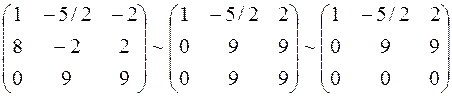
Вычитая из 2-ой строки 3-ью, получим нулевую строку, которую можно вычеркнуть. Таким образом, ранг системы равен 2, а число переменных 3. За свободную переменную возьмем 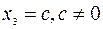. Тогда

.

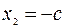
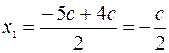Собственный вектор, соответствующий собственному числу 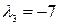, будет иметь вид

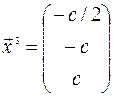или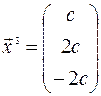

Покажем, что векторы 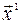и 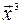ортогональны. Найдем их скалярное произведение

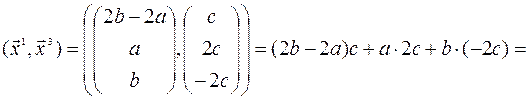
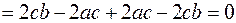
Заметим, что из множества собственных векторов, соответствующих равным собственным числам 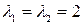, можно выбрать пару ортогональных векторов. Например, при 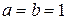имеем 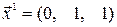, а при 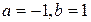, соответственно, 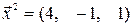. Найдем скалярное произведение этих векторов

,

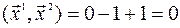т.е. эти векторы ортогональны.

Квадратичной формой с переменными 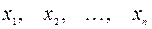называется функция

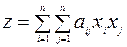, (4.4)

где 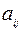-числа.

Пример 4.9. Рассмотрим квадратичную форму трех переменных

.

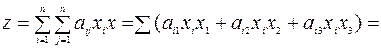
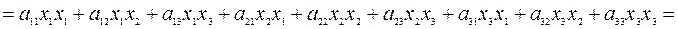
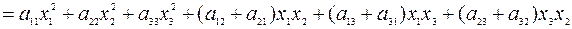Введем обозначения

, , .

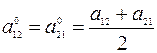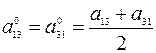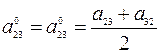Тогда квадратичная форма примет вид

.

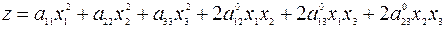Введем квадратную симметрическую матрицу и вектор :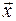

,

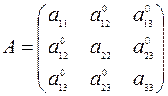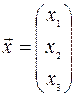
Тогда квадратичную форму можно записать в виде

.

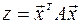Проверим это:

.

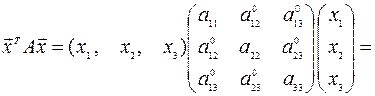
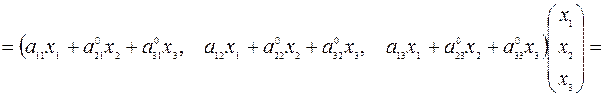
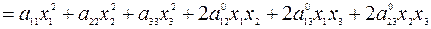Очевидно, что любую квадратичную форму (4.4) можно записать в матрично-векторном виде

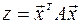, (4.5)

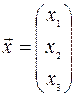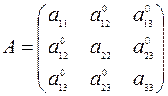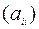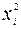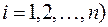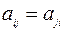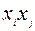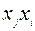где , - симметрическая матрица, в которой элементы являются коэффициентами при (при всех и равны полусуммам коэффициентов при членах, содержащих произведения и (при всех .

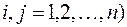Такая матрица называется матрицей квадратичной формы.

Квадратичные формы, все коэффициенты 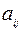которых вещественные числа, называются вещественными.

Матрица вещественной квадратичной формы является вещественной симметрической матрицей. Далее будем рассматривать только вещественные квадратичной формы.

Для любой симметрической матрицей 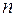-го порядка существует единственная квадратичная форма 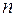переменных (эти квадратичные формы могут отличаться только обозначениями переменных).

Пример 4.10. Записать в матрично-векторном виде квадратичную форму

.

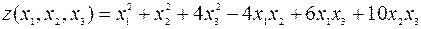Решение. Заметим, что в данной квадратичной форме подобные числа (содержащие 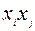и 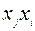) приведены, поэтому

, , ,

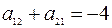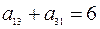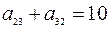откуда

, ,

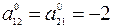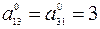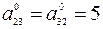
Таким образом, матрица данной квадратичной формы:

,

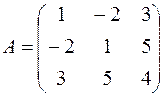а матрично-векторная запись данной квадратичной формы имеет вид:

.

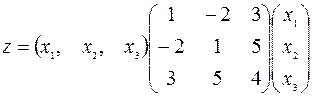Областью определения квадратичной формы 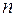переменных служит множество 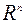всех 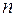-мерных векторов (будем рассматривать только вещественные векторы), а множеством значений - некоторое множество вещественных чисел. Во многих практических, в том числе и экономических, задачах квадратичная форма описывает, например, прибыль или затраты ресурсов. При этом важно знать, при каких условиях квадратичная форма принимает только положительные или только неотрицательные значения

Квадратичная форма (и ее матрица) называется положительно (отрицательно) определенной, если она принимает положительные (отрицательные) значения на всех ненулевых векторах.

Квадратичная форма (и ее матрица) называется положительно (отрицательно) определенной, если она принимает положительные (отрицательные) значения на всех ненулевых векторах.

Квадратичная форма (и ее матрица) называется неопределенной, если она принимает положительные значения на одних векторах и отрицательные - на других.

Пример 4.11. Выяснить, являются ли положительно (или отрицательно) определенными следующие квадратичные формы

a) ;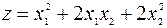

b) ;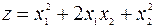

c) ;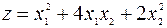

Решение. Преобразуем данные формы:

a) 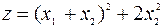, форма положительна определенная;

b) 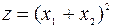, форма неотрицательно определенная, она принимает нулевое значение, например, на векторе ;

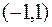c) 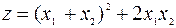, форма неопределенная, она принимает положительное значение, например, на векторе 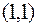и отрицательное на векторе ;

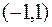Если квадратичная форма содержит только квадраты переменных, то говорят, что она имеет канонический вид.

Если вместо переменных 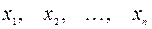ввести новые переменные 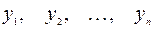путем линейного преобразования 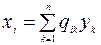, то получим иной вид квадратичной формы .

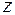Приведем без доказательства основную теорему о квадратичных формах.

Теорема 4.5. Любая квадратичная форма может быть приведена некоторым линейным преобразованием к каноническому виду.

Канонический вид данной квадратичной формы определен неоднозначно, т.е. если канонический вид данной квадратичной формы таков: 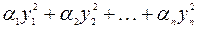(число не равных нулю коэффициентов в этом выражении равно рангу матрицы данной квадратичной формы), то коэффициенты 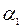, , 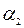…, 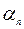определяются единственным образом. В частности, если все собственные числа 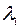, , 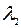…, 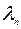матрицы квадратичной формы различны, т.е. ранг этой матрицы равен числу переменных, то канонический вид данной квадратичной формы может быть записан так: .

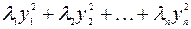Это позволяет сформулировать следующую теорему

Теорема 4.6. Вещественная квадратичная форма является положительно (неотрицательно) определенной в тои и только в том случае, если все собственные числа матрицы этой квадратичной формы является положительны (неотрицательны). Квадратичная форма является неопределенной, если среди собственных чисел её матрицы есть как положительные, так и отрицательные.

С помощью этой теоремы невозможно определить, является ли данная квадратичная форма является положительно определенной, по её коэффициентам, так как для этого необходимо найти собственные числа её матрицы. Следующая теорема позволяет ответить на поставленный вопрос, если известен любой канонический вид данной матрицы.

Теорема 4.7 (закон инерции квадратичных форм).

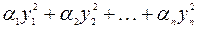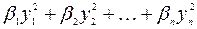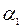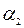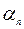
Если для некоторой квадратичной формы получены два различных канонических вида и , то число положительных (отрицательных) чисел среди коэффициентов , , …, 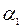и среди коэффициентов 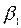, , 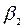…, 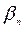одно и то же.

Однако, и теорема 4.7 не дает возможности определить, является ли данная квадратичная форма положительно или отрицательно определенной, непосредственно по коэффициентам квадратичной формы. Сделать это позволяет теорема 4.8, которую мы также приведем без доказательства после того, как введем следующие понятия.

Главными подматрицами квадратной матрицы 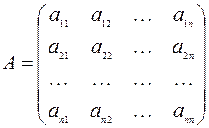называются матрицы

, , …, .

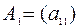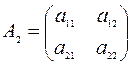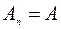Определители главных подматриц называются главными минорами квадратной матрицы. Обозначим их так , , …, .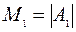

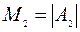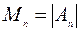Теорема 4. 8. Вещественная квадратичная форма является положительно (отрицательно) определенной в том и только в том случае, если все главные миноры матрицы этой квадратичной формы положительны (имеют чередующиеся знаки, начиная с минуса у главного минора первого порядка, т. е. у элемента ).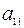

Пример 4.12. Выяснить, является ли положительно (или отрицательно) определенной квадратичная форма .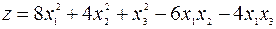

Решение. Напишем матрицу данной квадратичной формы и вычислим ее главные миноры:

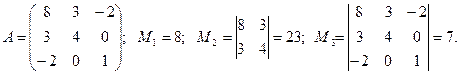
Все главные миноры матрицы данной квадратичной формы положительны, следовательно, данная квадратичная форма является положительно определенной.