Укажем свойства собственных чисел матрицы квадратной матрицы.
1.Сумма собственных чисел матрицы А равна следу этой матрицы (т.е. сумме её диагональных элементов)
Проверим это свойство на матрице из примера 4.1.
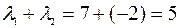
След матрицы А равен 3+2=5.
2.Произведение собственных чисел матрицы А равно определителю этой матрицы.
В нашем примере 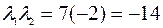 ;
; 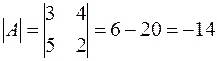 .
.
3.Число отличных от нуля собственных чисел матрицы А равно её рангу. В частности, все собственные числа матрицы А отличны от нуля в том и только том случае, если матрица А - невырожденная.
Пример 4.4.Найти все собственные числа матрицы А
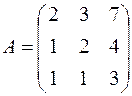
Решение. Составим характеристическое уравнение данной матрицы
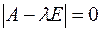
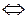
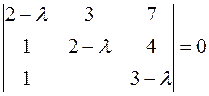
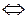
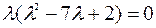
Матрица А имеет три собственных числа
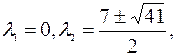
два из которых не равны нулю. Ранг матрицы также равен 2. Действительно,
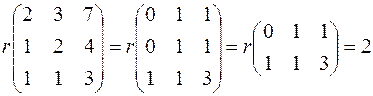
4.Если 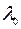 собственное число невырожденной матрицы
собственное число невырожденной матрицы  , то
, то 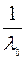 - собственное число матрицы
- собственное число матрицы 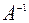 .
.
Докажем это свойство.
Пусть 
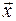 - собственный вектор матрицы
- собственный вектор матрицы  , соответствующий
, соответствующий 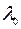 собственному числу
собственному числу 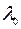 . Тогда справедливо равенство
. Тогда справедливо равенство 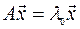 . Так как матрица
. Так как матрица 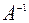 существует, умножим на неё обе части равенства, получим
существует, умножим на неё обе части равенства, получим
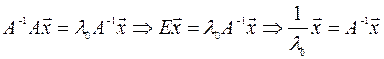 .
.
Это означает, что 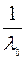 есть собственное число матрицы
есть собственное число матрицы 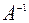 , а вектор
, а вектор 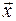 - соответствующий ему собственный вектор. Свойство доказано.
- соответствующий ему собственный вектор. Свойство доказано.
5.Если 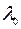 . - собственное число матрицы
. - собственное число матрицы  , то
, то 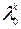 . - собственное число матрицы
. - собственное число матрицы 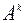 при любом целом
при любом целом 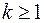 .
.
Докажем это свойство методом индукции.
Сначала проверим его справедливость при 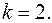 Пусть
Пусть 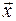 - собственный вектор матрицы
- собственный вектор матрицы  , соответствующий собственному числу
, соответствующий собственному числу 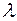 . Тогда
. Тогда
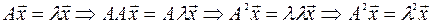
т.е. 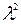 - собственное число матрицы
- собственное число матрицы 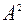 .
.
Допустим, что это свойство справедливо при показателе степени, равном 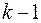 , т.е.
, т.е.
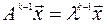
и докажем, что оно верно при показателе степени, равном 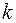 .
.
Умножив обе части последнего равенства на  , получим
, получим
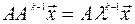 или
или 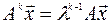
Поскольку 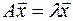 , то
, то 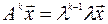 и окончательно
и окончательно 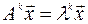 , т.е. число
, т.е. число 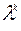 . является собственным числом матрицы
. является собственным числом матрицы 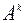 . Свойство доказано.
. Свойство доказано.
Квадратные матрицы одного порядка, имеющие одинаковые спектры, называются подобными.
6.Квадратные матрицы 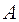 и
и 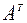 подобны.
подобны.
Для доказательства убедимся, что справедливо равенство
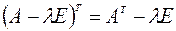 .
.
В силу свойств 4 и действий с матрицами
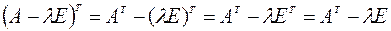 .
.
Следовательно, 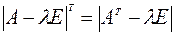 , т.е. матрицы
, т.е. матрицы 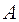 и
и 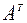 имеют одно и то же характеристическое уравнение, и, соответственно, одно и то же множество собственных чисел.
имеют одно и то же характеристическое уравнение, и, соответственно, одно и то же множество собственных чисел.
Заметим, что собственные векторы матриц 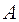 и
и 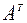 , соответствующие одинаковым собственным числам этих матриц, вообще говоря, различны. Покажем это на примере.
, соответствующие одинаковым собственным числам этих матриц, вообще говоря, различны. Покажем это на примере.
Пример 4.5. В примерах 4.1 и 4.3 были найдены собственные числа и собственные векторы матрицы 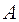 . Найти собственные числа и собственные векторы матрицы
. Найти собственные числа и собственные векторы матрицы 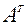 .
.
Решение.Матрица 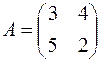 имеет собственные числа
имеет собственные числа 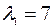 и
и 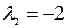 , соответствующие им векторы
, соответствующие им векторы 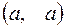 и
и 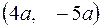 ,
, 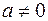 . Рассмотрим матрицу
. Рассмотрим матрицу 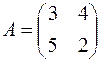 , найдем её собственные числа, решив уравнение
, найдем её собственные числа, решив уравнение 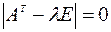
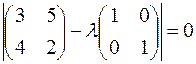 ,
, 
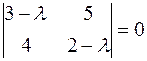 ;
;
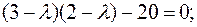
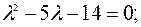
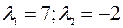
Итак, 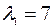 и
и 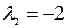 , т.е. матрица
, т.е. матрица 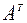 имеет тот же спектр, что и матрица
имеет тот же спектр, что и матрица  .
.
Найдем собственные векторы матрицы 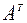 . Собственный вектор
. Собственный вектор 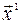 , соответствующий собственному числу
, соответствующий собственному числу 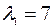 , находим, решая систему уравнений
, находим, решая систему уравнений
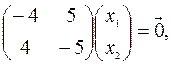
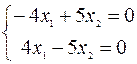
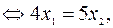
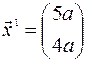 ,
, 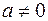 .
.
Собственный вектор 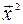 , соответствующий собственному числу
, соответствующий собственному числу 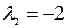 , находим, решая систему уравнений
, находим, решая систему уравнений
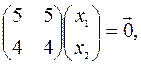
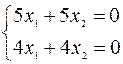
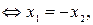
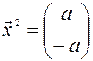 ,
, 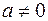 .
.
Итак, матрицы  и
и 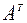 подобны, а собственные векторы, соответствующие равным собственным числам этих матриц, различны.
подобны, а собственные векторы, соответствующие равным собственным числам этих матриц, различны.
Следует отметить, что задача нахождения собственных чисел матрицы 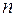 -го порядка, которая, как мы убедились, требует решения алгебраического уравнения
-го порядка, которая, как мы убедились, требует решения алгебраического уравнения 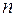 -й степени, при
-й степени, при 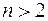 становится очень сложной. Однако, собственные числа диагональной матрицы найти легко.
становится очень сложной. Однако, собственные числа диагональной матрицы найти легко.
Теорема 4.2. Собственными числами диагональной матрицы являются числа, стоящие на её главной диагонали.
Доказательство. Диагональная матрица 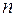 -го порядка имеет вид
-го порядка имеет вид
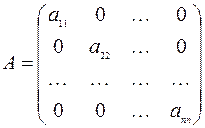 .
.
Характеристическое уравнение матрицы  таково:
таково:
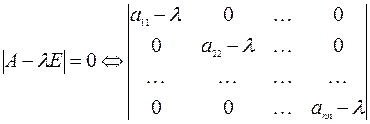
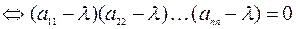
Корнями этого уравнения и, следовательно, собственными числами матрицы  являются числа
являются числа 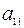 ,
, 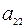 , … ,
, … , 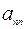 . Теорема доказана.
. Теорема доказана.
В следующих двух теоремах устанавливается, что для любой квадратной матрицы существует подобная ей диагональная матрица.
Теорема 4.3. Если  - квадратная матрица порядка
- квадратная матрица порядка 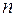 , а
, а 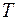 - невырожденная квадратная матрица того же порядка, то матрица
- невырожденная квадратная матрица того же порядка, то матрица 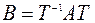 подобна
подобна  .
.
Доказательство. Достаточно показать, что характеристические уравнения матриц  и
и 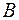 равносильны. Докажем сначала следующее тождество:
равносильны. Докажем сначала следующее тождество:
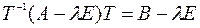 .
.
Действительно,
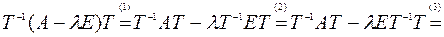
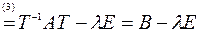 .
.
Равенство (1) верно ввиду дистрибутивности умножения матриц относительно сложения матриц. Равенство (2) следует из коммутативности умножения матрицы на единичную матрицу, а равенство (3) - из определения обратной матрицы.
С учетом доказанного тождества и свойства определителей получим
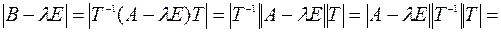
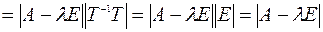 .
.
Следовательно, 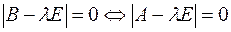 . Теорема доказана.
. Теорема доказана.
Теорема 4.4(о приведении квадратной матрицы к диагональному виду).
Пусть все собственные числа квадратной матрицы  различны,
различны, 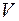 - квадратная матрица, столбцами которой являются собственные векторы матрицы
- квадратная матрица, столбцами которой являются собственные векторы матрицы  , соответствующие разным собственным числам этой матрицы, тогда матрица
, соответствующие разным собственным числам этой матрицы, тогда матрица 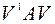 -диагональная матрица, подобная матрице
-диагональная матрица, подобная матрице  .
.
Заметим, что найти собственные числа квадратной матрицы, применяя теорему 4.4, можно только в том случае, если известны собственные векторы этой матрицы. Вместе с тем теорема 4.4 используется во многих теоретических выводах.
Пример 4.6. В примерах 4.1 и 4.3были найдены собственные числа и собственные векторы матрицы:
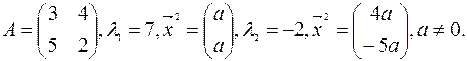
Показать справедливость равенства 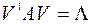 , где
, где 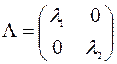
Решение. В нашем примере
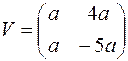
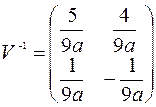
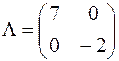
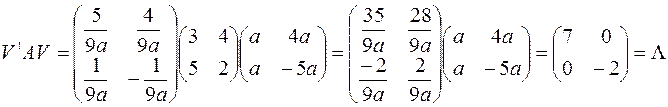 Рассмотрим свойства собственных векторов матрицы.
Рассмотрим свойства собственных векторов матрицы.
1.Собственные векторы матрицы, соответствующие её различным собственным числам, линейно независимы. Опуская доказательство этого свойства, проверим его на примере.
Пример 4.7. В примере 4.3 были найдены собственные векторы матрицы  , соответствующие разным собственным числам:
, соответствующие разным собственным числам:
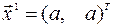 ,
, 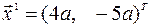 ,
, 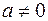 .
.
Показать, что эти векторы линейно независимы.
Решение. Составим систему линейных уравнений
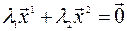
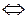
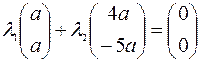
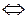
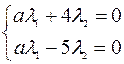 .
.
Определитель матрицы этой однородной системы линейных уравнений не равен нулю:
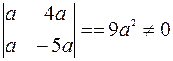
Следовательно, система имеет только нулевое решение, т.е. векторы 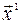 и
и 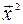 линейно независимы.
линейно независимы.
2.Если все собственные числа квадратной матрицы 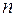 -го порядка различны, то соответствующие им собственные векторы образуют базис пространства
-го порядка различны, то соответствующие им собственные векторы образуют базис пространства 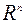 .
.
Это следует из предыдущего свойства о определения базиса пространства 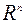 .
.
3.Любая не равная нулевому вектору линейная комбинация собственных векторов данной матрицы, соответствующих одному и тому же собственному числу этой матрицы, также является собственным вектором данной матрицы.
Докажем это свойство.
Пусть 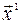 ,
, 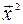 ,… ,
,… , 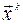 - собственные векторы матрицы
- собственные векторы матрицы  , соответствующие её собственному числу
, соответствующие её собственному числу 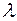 , а
, а 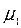 ,
, 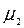 , …
, … 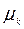 - произвольные числа, такие, что
- произвольные числа, такие, что

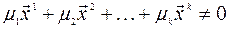 .
.
По условию 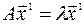 ,
, 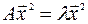 ,…,
,…, 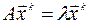 , тогда
, тогда
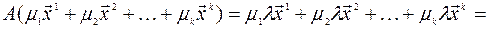
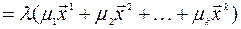 .
.
Это означает, что вектор 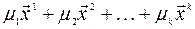 является собственным вектором матрицы
является собственным вектором матрицы  , соответствующим её собственному числу
, соответствующим её собственному числу 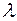 .
.
Дата добавления: 2015-09-29; просмотров: 9199;
