Абсолютная величина и норма матрицы.
Под абсолютной величиной (модулем) матрицы 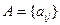 понимается матрица
понимается матрица 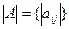 , где все элементы
, где все элементы 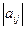 - модули элементов матрицы A.
- модули элементов матрицы A.
Пусть А и В матрицы, для которых операции А+В и АВ имеют смысл. Тогда
1. 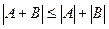 .
.
2. 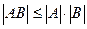 .
.
3. 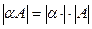 .
.
Под нормой матрицы 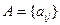 понимается действительное число
понимается действительное число 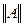 , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям:
1. 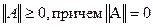 тогда и только тогда, когда А=0.
тогда и только тогда, когда А=0.
2. 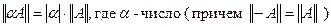
3. 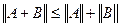
4. 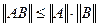
5. 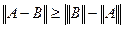 , где А и В матрицы, для которых соответствующие операции имеют смысл.
, где А и В матрицы, для которых соответствующие операции имеют смысл.
Норму матрицы можно определить по-разному. Для матрицы 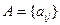 произвольного размера рассмотрим три следующие легко вычисляемые нормы:
произвольного размера рассмотрим три следующие легко вычисляемые нормы:
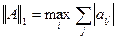 - максимальная сумма модулей элементов матрицы по строкам.
- максимальная сумма модулей элементов матрицы по строкам.
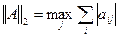 - максимальная сумма модулей элементов матрицы по столбцам.
- максимальная сумма модулей элементов матрицы по столбцам.
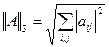 - корень квадратный из суммы квадратов модулей всех элементов матрицы.
- корень квадратный из суммы квадратов модулей всех элементов матрицы.
Пример 1.Для матрицы 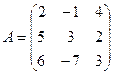
Вычислить все вышеперечисленные нормы матрицы.
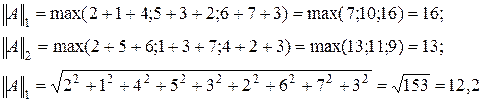
Дата добавления: 2015-10-05; просмотров: 3717;
