Решая эту систему методом Гаусса, получим
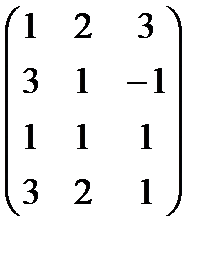
 ~
~ 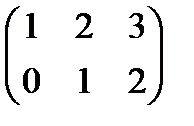 ,
,
откуда найдем бесчисленное множество решений 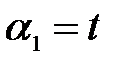 ,
, 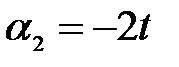 ,
, 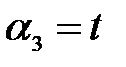 , где t - произвольное вещественное число. Итак, для данных векторов условие (3.8) выполняется не только при
, где t - произвольное вещественное число. Итак, для данных векторов условие (3.8) выполняется не только при 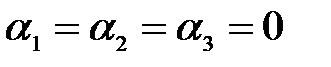 , но и, например, при
, но и, например, при 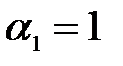 ,
, 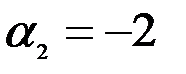 ,
, 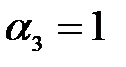 (при
(при 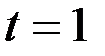 ), при
), при 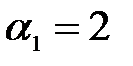 ,
, 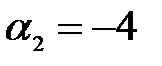 ,
, 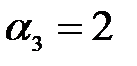 (при
(при 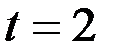 ). Следовательно, эти векторы линейно зависимы.
). Следовательно, эти векторы линейно зависимы.
Пример 3.10.Выяснить, будет ли линейно зависимой система векторов:
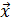 1 = (1, 1, 4, 2),
1 = (1, 1, 4, 2),
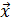 2 = (1, -1, -2, 4),
2 = (1, -1, -2, 4),
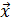 3 = (0, 2, 6, -2),
3 = (0, 2, 6, -2),
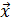 4 = (-3, -1, 3, 4),
4 = (-3, -1, 3, 4),
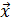 5 = (-1, 0, - 4, -7).
5 = (-1, 0, - 4, -7).
Решение.Система векторов является линейно зависимой, если найдутся такие числа α1, α2, α3, α4, α5, из которых хотя бы одно отлично от нуля, что выполняется векторное равенство:
α1 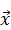 1+ α2
1+ α2 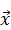 2+ α3
2+ α3 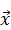 3+ α4
3+ α4 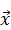 4+ α5
4+ α5 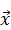 5=
5= 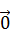 .
.
В координатной записи оно равносильно системе уравнений:
α1 + α2 - 3 α4 - α5= 0,
α1- α2 + 2 α3 - α4 = 0,
4 α1 - 2 α2 + 6 α3 +3 α44 - 4 α5 = 0,
2 α1 + 4 α2 - 2 α3 + 4 α4 - 7 α5= 0.
Итак, получили систему линейных однородных уравнений. Решаем ее методом исключения неизвестных:
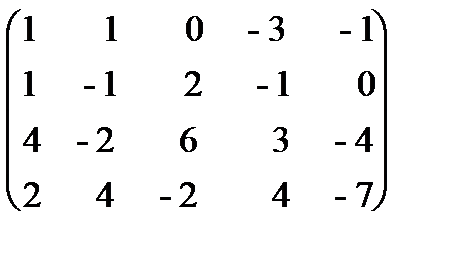 ~
~  ~
~ 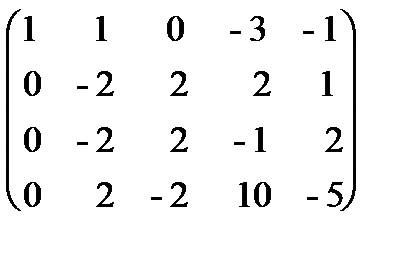 ~
~
~  ~
~  ~
~ 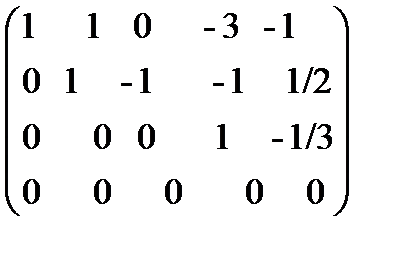 .
.
Система приведена к ступенчатому виду, ранг матрицы равен 3, значит, однородная система уравнений имеет решения, отличные от нулевого (r < n). Определитель при неизвестных x1, x2, x4 отличен от нуля, поэтому их можно выбрать в качестве базисных и продолжить обнуление элементов во втором и четвертом столбцах:
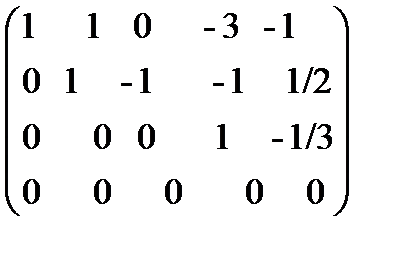 ~
~ 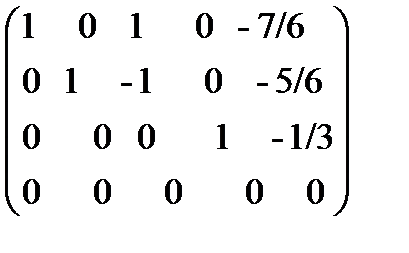
Имеем: α4 = 1/3 t, α2 = 5/6 t+ s, α1 = 7/6 t – s, α3=s, α5=t, где s, t - произвольные вещественные числа.
Система имеет бесчисленное множество решений; если свободные неизвестные α3 и α5 не равны нулю одновременно, то и базисные неизвестные отличны от нуля. Следовательно, векторное уравнение
α1 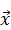 1+ α2
1+ α2 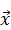 2+ α3
2+ α3 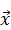 3+ α4
3+ α4 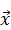 4+ α5
4+ α5 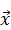 5= 0.
5= 0.
имеет коэффициенты, не равные нулю одновременно; пусть например, α 5 = 6, α 3 =1. Тогда α 4=2, α 2 = 6, α 1=6 и мы получим соотношение
6 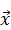 1 + 6
1 + 6 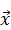 2 +
2 + 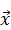 3 + 2
3 + 2 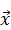 4 + 6
4 + 6 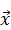 5 = 0,
5 = 0,
т.е. данная система векторов линейно зависима.
Дата добавления: 2015-09-29; просмотров: 865;
