Базис и размерность векторного пространства
Фундаментальным вопросом теории векторных пространств является вопрос о том, можно ли, а если можно, то как, произвольный вектор пространства представить в виде линейной комбинации фиксированного набора векторов из этого пространства. Далее мы получим ответ на этот вопрос.
Система линейно независимых векторов 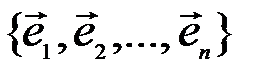 векторного пространства
векторного пространства 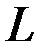 называется базисом этого пространства, если любой вектор из
называется базисом этого пространства, если любой вектор из 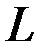 может быть представлен в виде линейной комбинации векторов этой системы, т.е. для каждого вектора
может быть представлен в виде линейной комбинации векторов этой системы, т.е. для каждого вектора 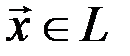 существуют вещественные числа
существуют вещественные числа 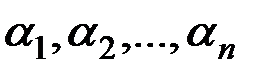 такие, что имеет место равенство
такие, что имеет место равенство
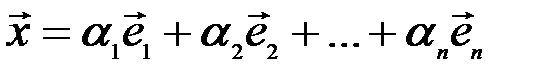 .
.
Это равенство называется разложением вектора 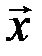 по базису
по базису 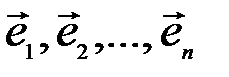 , а числа
, а числа 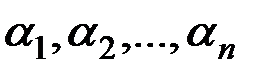 называются координатами вектора
называются координатами вектора 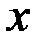 относительно базиса(илив базисе)
относительно базиса(илив базисе) 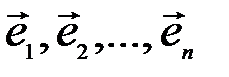 .
.
Упражнение. Докажите, что базис является максимальным линейно независимым набором векторов: любой набор, содержащий его как собственное подмножество, линейно зависим.
Пример 3.11. В базисе 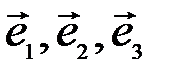 заданы векторы
заданы векторы 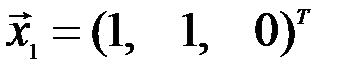 ,
, 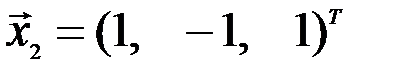 и
и 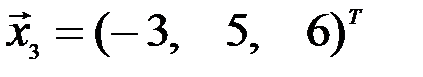 . Показать, что векторы
. Показать, что векторы 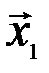 ,
, 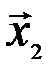 и
и 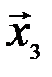 образуют базис.
образуют базис.
Решение. Векторы 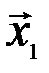 ,
, 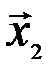 и
и 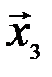 образуют базис, если они линейно независимы. Составим векторное равенство
образуют базис, если они линейно независимы. Составим векторное равенство
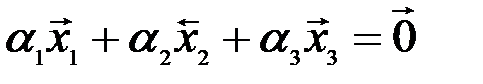 .
.
В координатной записи оно равносильно системе уравнений:
α1 + α2 - 3 α3= 0,
α1 - α2 + 5 α3 = 0,
α2 + 6 α3 = 0,
Решая его аналогично примеру 3.10, можно убедиться в единственном нулевом его решении 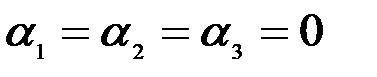 ,т.е. векторы
,т.е. векторы 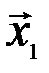 ,
, 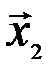 и
и 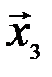 образуют систему линейно независимых векторов, и, следовательно, составляют базис.
образуют систему линейно независимых векторов, и, следовательно, составляют базис.
Теорема 3.5. (о единственности разложения по базису). Каждый вектор 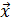 пространства
пространства 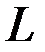 может быть разложен по базису
может быть разложен по базису 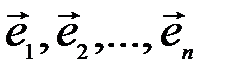 единственным образом, т.е. координаты каждого вектора
единственным образом, т.е. координаты каждого вектора 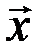 в базисе
в базисе 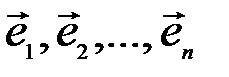 определяются однозначно.
определяются однозначно.
Доказательство. Допустим, что для некоторого элемента 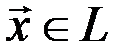 существуют два разложения по одному и тому же базису:
существуют два разложения по одному и тому же базису:
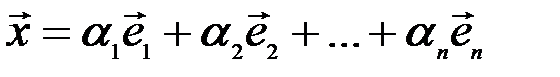 и
и 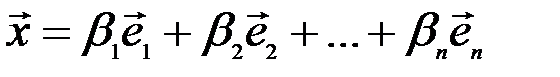 .
.
Дата добавления: 2015-09-29; просмотров: 1249;
