Теорема доказана.

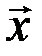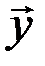В любом вещественном евклидовом пространстве можно ввести понятие угла между двумя произвольными элементами и этого пространства. Аналогично тому, как это делается в п.3.1 (векторы на плоскости и в пространстве), мы назовем углом 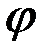между элементам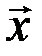и и 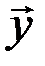тот угол (изменяющийся в пределах от до 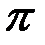), косинус которого определяется соотношением

.

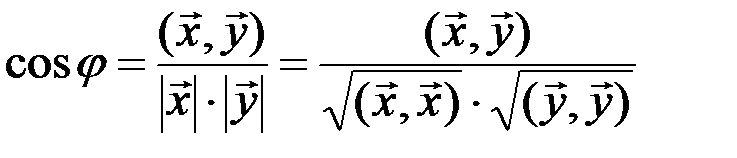Данное нами определение угла корректно, ибо в силу неравенства Коши-Буняковского (3.11) дробь, стоящая в правой части последнего равенства, по модулю не превосходит единицы.

Будем называть два произвольных элемента 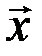и 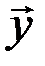евклидова пространства 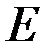ортогональными, если их скалярное произведение равно нулю 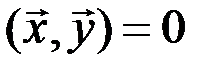(в этом случае ).

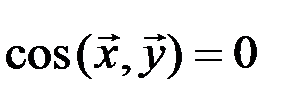Очевидно, что нулевой вектор ортогонален любому вектору.

Снова проводя аналогию с геометрическими объектами, назовем сумму 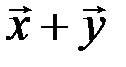двух ортогональных элементов и 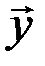гипотенузой прямоугольного треугольника, построенного на элементах и .

Во всяком евклидовом пространстве справедлива теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В самом деле, поскольку 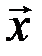и ортогональны, а, следовательно, 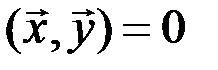, то в силу аксиом и определения нормы верно равенство

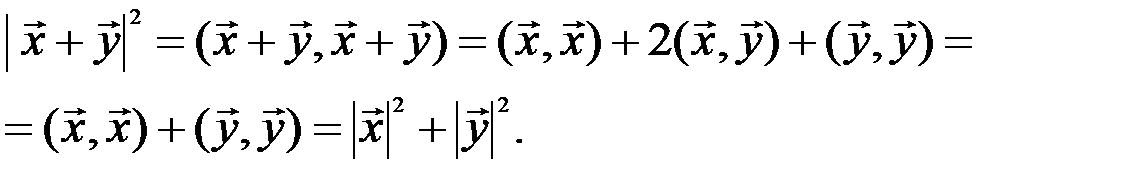
Ранее было введено понятие базиса 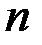-мерного векторного пространства. Все базисы в произвольном векторном пространстве являлись равноправными, и у нас не было оснований предпочитать один базис другому. В евклидовом пространстве существуют специальные, особо удобные базисы, называемые ортонормированными базисами. Эти базисы играют ту же роль, что и декартов прямоугольный базис в аналитической геометрии.

Говорят, что 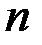элементов 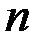-мерного евклидова пространства 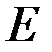образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из них равна единице, т.е. если

(3.12)

Для того чтобы установить корректность определения, следует доказать, что входящие в это определение векторы 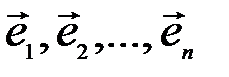образуют один из базисов 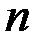-мерного пространства 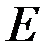. А для этого (в силу теоремы о связи между понятиями базиса и размерности) достаточно доказать, что эти элементы линейно независимы, т.е. равенство

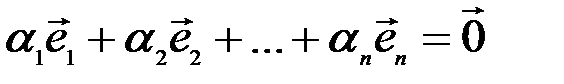(3.13)

возможно лишь при .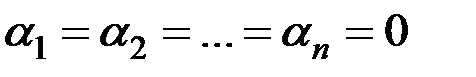

Докажем это. Пусть – любой из номеров . Умножая равенство (3.13) скалярно на элемент 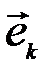, получим

,

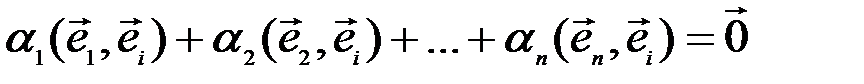откуда, учитывая, 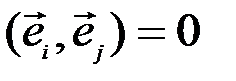при и что 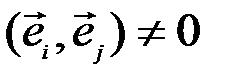при всех 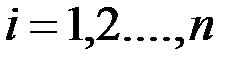, мы получим, что 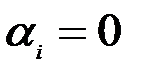при всех .

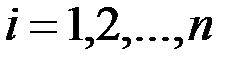Ценность понятия ортонормированного базиса была бы невелика, если бы не следующая теорема.

Теорема 3.11. Во всяком 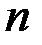-мерном евклидовом пространстве существует ортонормированный базис.(Без доказательства)

Произвольный ортонормированный базис любого евклидова пространства обладает свойствами, аналогичными свойствам декартова прямоугольного базиса (на плоскости и в пространстве геометрических векторов). Так, например, в ортонормированном базисе скалярное произведение двух любых векторов равно сумме произведений соответствующих координат этих векторов.

Примером ортонормированного базиса в пространстве 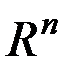является система 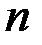векторов, у которых 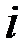-ая компонента равна единице, а остальные равны нулю:

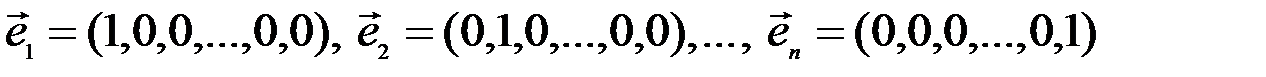
Еще раз подчеркнем, что существенным отличием произвольных векторных пространств от их частного случая, евклидовых пространств, является то, что в векторном пространстве не определены метрические соотношения между его элементами.