Интегральная теорема Коши для многосвязной области.
Определение. Область D называется правильной, если D ограниченная область и её граница 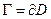 состоит из конечного числа попарно не пересекающихся простых, замкнутых, спрямляемых кривых.
состоит из конечного числа попарно не пересекающихся простых, замкнутых, спрямляемых кривых.
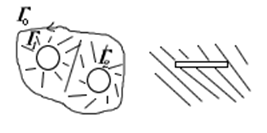
Т.е. слева правильная область (конечное число дырок), а справа не правильная область (область с разрезом).
Границы правильной области ориентированны положительно, если при обходе границы область остаётся слева.
Теорема4. Если 1) D - правильная область с положительно ориентированной границей Г.
2) f(z) – голоморфна в 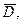 тогда
тогда 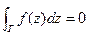 .
.
Доказательство. (Как ориентированна граница в принципе не важно, важно, что ориентированна). Проведём разрезы в каждом направлении. Вырежем 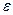 - окрестности этих разрезов, тогда область
- окрестности этих разрезов, тогда область 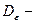 это правильная жорданова область и её граница имеет следующий вид:
это правильная жорданова область и её граница имеет следующий вид: 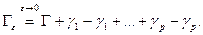 По теореме2
По теореме2 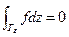 . Но по свойству аддитивности:
. Но по свойству аддитивности: 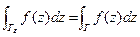 т.к.
т.к. 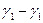 и т.д. сокращаются.
и т.д. сокращаются. 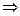 доказано.
доказано. 
Но это не строгое доказательство. Его можно считать строгим только для гладких кривых, в остальных случаях мы не знаем топологических подробностей. 
Замечание. Справедливо усиление теоремы, когда f(z) – голоморфна в 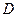 и непрерывна в
и непрерывна в 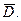
Дата добавления: 2015-09-02; просмотров: 1578;
