Вторая теорема Вейерштрасса.

Теорема. Если 1) D – ограниченная область с границей .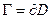

2) 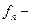голоморфна в области D, непрерывна в .

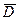3) 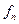сходится равномерно на Г. То 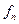сходится равномерно внутри D.

Доказательство. Мы докажем, что 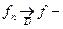равномерно. Проверим критерий Коши: 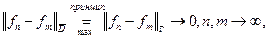по условию.

СТЕПЕННЫЕ РЯДЫ