В силу аксиом 1) – 3) последнее неравенство можно переписать в виде
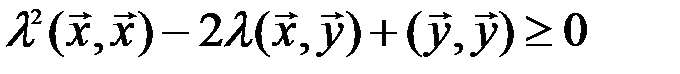 .
.
Необходимым и достаточным условием неотрицательности последнего квадратного трехчлена является неположительность его дискриминанта 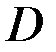 :
:
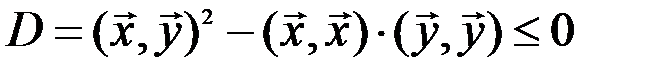 .
.
Из неравенства 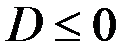 сразу же следует неравенство Коши-Буняковского.
сразу же следует неравенство Коши-Буняковского.
В том случае, когда 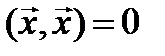 квадратный трехчлен
квадратный трехчлен 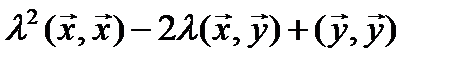 вырождается в линейную функцию. Но в этом случае элемент
вырождается в линейную функцию. Но в этом случае элемент 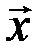 является нулевым, так что
является нулевым, так что 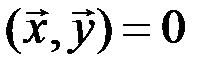 , и неравенство
, и неравенство 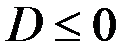 также справедливо. Теорема доказана.
также справедливо. Теорема доказана.
Наша очередная задача – ввести в произвольном евклидовом пространстве понятие нормы (или длины) каждого элемента. Для этого введем понятие нормированного пространства.
Векторное пространство 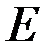 называется нормированным, если выполнены следующие два требования:
называется нормированным, если выполнены следующие два требования:
I. Имеется правило, посредством которого каждому элементу 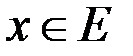 ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое символом
ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое символом 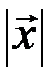 .
.
II. Указанное правило подчинено следующим трем аксиомам:
1) 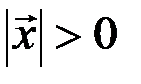 , если
, если 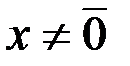 ;
; 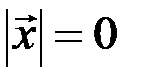 , если
, если 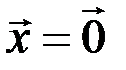 ;
;
2) 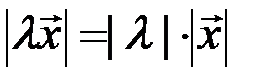
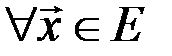 ,
, 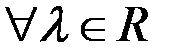 ;
;
3) 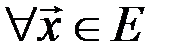

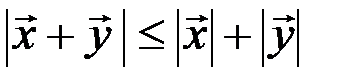 (неравенство треугольника).
(неравенство треугольника).
Теорема 3.10. Всякое евклидово пространство является нормированным, если в нем норму любого элемента 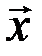 определить равенством
определить равенством
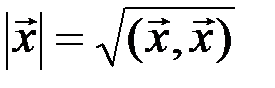 . (3.10)
. (3.10)
Доказательство. Достаточно доказать, что для нормы, определенной соотношением (3.10), справедливы аксиомы 1) – 3) из определения нормированного пространства.
Справедливость для нормы аксиомы 1) следует из аксиомы 4) скалярного произведения. Справедливость для нормы аксиомы 2) следует из аксиом 1) и 3) скалярного произведения.
Остается убедиться в справедливости для нормы аксиомы 3), т.е. неравенства треугольника. Воспользуемся неравенством Коши-Буняковского, которое перепишем в виде
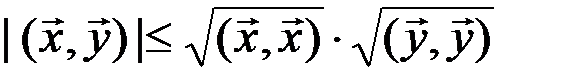 . (3.11)
. (3.11)
С помощью последнего неравенства, аксиом скалярного произведения и равенства (3.10), получаем
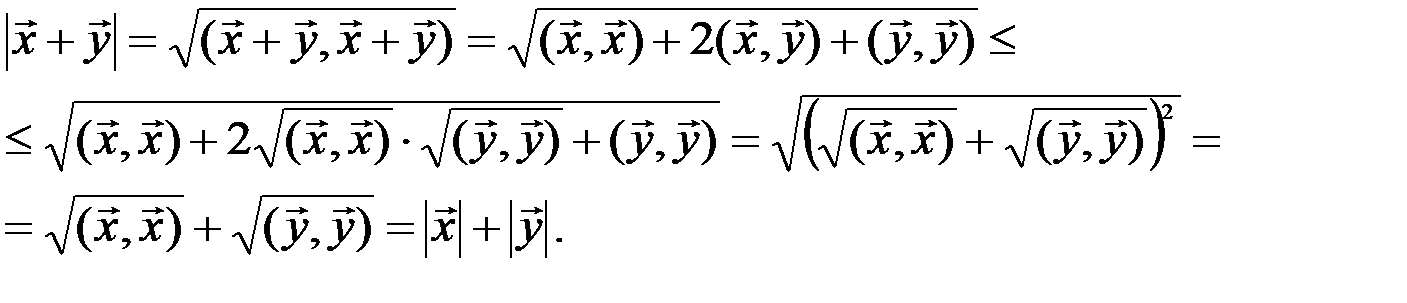
Дата добавления: 2015-09-29; просмотров: 1103;
