Евклидовы пространства
В разделе 3.1 вводится понятие скалярного произведения двух векторов (на плоскости или в пространстве), которое обладает четырьмя основными свойствами. Мы рассмотрим векторные пространства произвольной природы, для элементов которых каким-либо способом (причем, безразлично каким) определено правило, ставящее в соответствие любым двум элементам число, называемое скалярным произведением этих элементов. При этом важно только, чтобы это правило обладало теми же четырьмя свойствами, что и правило составления скалярного произведения для геометрических векторов на плоскости или в пространстве. Векторные пространства, в которых определено указанное правило, называются евклидовыми пространствами.
Дадим более строгое определение.
Вещественное векторное пространство 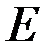 называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования:
называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования:
I. Имеется правило, посредством которого любым двум элементам этого пространства 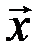 и
и 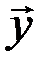 ставится в соответствие вещественное число, называемое скалярным произведением этих элементов (и обозначаемое символом
ставится в соответствие вещественное число, называемое скалярным произведением этих элементов (и обозначаемое символом 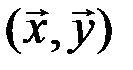 ).
).
II. Указанное правило подчинено следующим четырем аксиомам:
1) 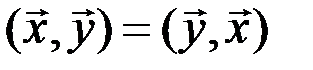 (коммутативность или симметрия);
(коммутативность или симметрия);
2) 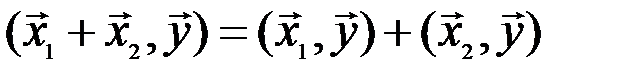 (дистрибутивность скалярного произведения относительно сложения);
(дистрибутивность скалярного произведения относительно сложения);
3) 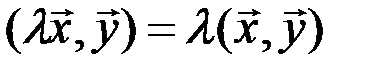
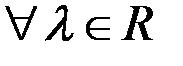 ;
;
4) 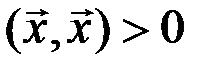 , если
, если 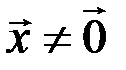 ;
; 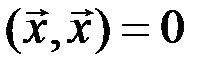 , если
, если 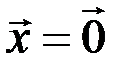 .
.
Пример 3.13. Рассмотрим векторные пространства 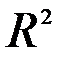 или
или 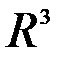 геометрических векторов на плоскости или в пространстве. Исследовать, являются ли данные пространства евклидовыми.
геометрических векторов на плоскости или в пространстве. Исследовать, являются ли данные пространства евклидовыми.
Решение. Скалярное произведение любых двух векторов определим стандартным образом (как произведение длин этих векторов на косинус угла между ними). В разделе 3.1 доказывается, что в этом случае выполняются аксиомы 1) – 4). Следовательно, пространства 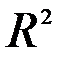 и
и 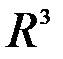 являются евклидовыми пространствами.
являются евклидовыми пространствами.
Пример 3.14. Исследовать, является ли 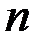 -мерное координатное пространство
-мерное координатное пространство 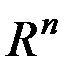 евклидовыми.
евклидовыми.
Решение. Если 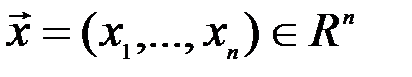 ,
, 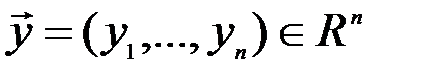 , то скалярное произведение
, то скалярное произведение 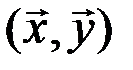 определим равенством
определим равенством
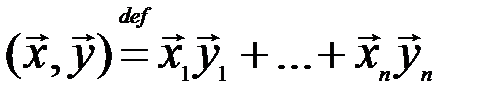 .
.
В этом случае выполнение аксиом 1) – 4) легко проверяется. Следовательно, пространство 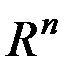 является евклидовым.
является евклидовым.
Cкалярное произведение векторов пространства 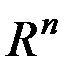 имеет и экономический смысл. Если, например, .
имеет и экономический смысл. Если, например, . 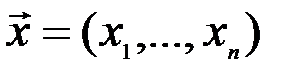 есть вектор объемов различных товаров, а
есть вектор объемов различных товаров, а 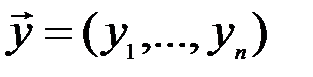 - вектор их цен, то
- вектор их цен, то 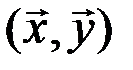 выражает суммарную стоимость этих товаров.
выражает суммарную стоимость этих товаров.
Следующая теорема справедлива для совершенно произвольного евклидова пространства как конечной, так и бесконечной размерности.
Теорема 3.9. Для любых двух элементов 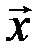 и
и 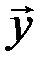 евклидова пространства справедливо неравенство
евклидова пространства справедливо неравенство
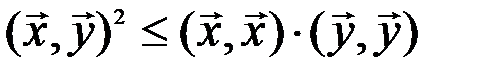 ,
,
называемое неравенством Коши-Буняковского.
Доказательство. Для любого вещественного числа 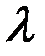 в силу аксиомы 4) скалярного произведения справедливо неравенство
в силу аксиомы 4) скалярного произведения справедливо неравенство
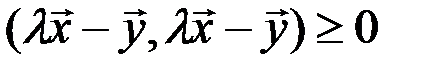 .
.
Дата добавления: 2015-09-29; просмотров: 897;
