Вектор из n-мерного векторного пространства называется пропорциональным вектору , если существует такое число k, что .

Лекция 6-7. Метод Гаусса решения систем линейных алгебраических уравнений. Матрица, расширенная матрица, ранг матрицы. Теорема Кронекера-Капелли. Решение однородных квадратных систем линейных алгебраических уравнений. Решение прямоугольных систем.

.

Линейная зависимость векторов.

Вектор из n-мерного векторного пространства называется пропорциональным вектору , если существует такое число k, что .

Обобщением понятия пропорциональности векторов служит следующее понятие: вектор 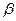называется линейной комбинацией векторов 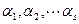, если существуют такие числа 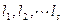, что

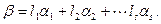
Система векторов 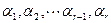называется линейно зависимой, если хотя бы один из этих векторов является линейной комбинацией остальных векторов, и линейно независимой – в противоположном случае.

Это определение можно дать в другом виде, а именно: система векторов 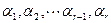линейно зависима, если существуют такие числа 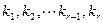, хотя бы одно из которых отлично от нуля, что имеет место равенство .

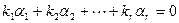Совершенно очевидно, что система векторов, содержащих два пропорциональных вектора или нулевой вектор, линейно зависима.

Ранг матрицы.

Строки или столбцы любой матрицы можно рассматривать как совокупность векторов. Поэтому к строкам и столбцам матрицы применимо вышеизложенное понятие линейной зависимости.

Рангом любой матрицы называется число линейно-независимых строк ( или столбцов ), содержащихся в этой матрице. Другими словами, рангом матрицы А называется максимальный порядок отличного от нуля минора этой матрицы. Ранг матрицы обозначается r(A). Как результат такого определения мы имеем:

1. Ранг матрицы равен нулю тогда и только тогда, когда рассматривается нулевая матрица. Во всех остальных случаях ранг матрицы представляет собой положительное число.

2. Ранг прямоугольной матрицы не превосходит меньшего из величин: количество строк и количество столбцов матрицы.

3. Ранг квадратной матрицы равен ее порядку или меньше его.

4. Если r(A)=r, тогда матрица А содержит по крайней мере один ненулевой минор порядка r, а все миноры более высокого порядка чем r, равны нулю.

5. Если ранг квадратной матрицы порядка n, меньше ее порядка, то у такой матрицы не существует обратной, а ее определитель равен нулю.

6. Ранг нулевой матрицы равен нулю, а ненулевой матрицы-строки (или столбца) равен единице.

Рассмотрим один из методов определения ранга матрицы, основанный на четвертом следствии из его определения. Этот метод носит название метода окаймления и состоит в нахождении ненулевого минора максимального порядка. При вычислении ранга матрицы с помощью этого метода переходят от миноров меньших порядков ( начиная с миноров первого порядка, т.е. элементов матрицы.) к минорам больших порядков, придерживаясь следующего правила: пусть найден минор r-го порядка М , отличный от нуля; тогда нужно вычислить лишь миноры (r+1)-го порядка, окаймляющие данный минор М . Если все эти миноры равны нулю, то ранг матрицы равен r; если же хотя бы один из них отличен от нуля, то эту операцию следует применить к нему, причем в этом случае ранг матрицы заведомо больше r.

Пример 1.Методом окаймления найти ранг матрицы

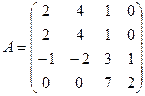
a) Выберем минор первого порядка, не равный нулю: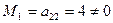

b) Найдем окаймляющий минор второго порядка, не равный нулю:

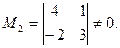
c) Рассмотрим все миноры третьего порядка, окаймляющие минор 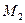, для чего составим миноры 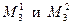из 2,3 и 4-й строк:

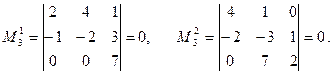
так как в этих минорах 3-я строка равна сумме 1-й строки и удвоенной 2-й.

Окаймляющие миноры из 1, 2 и 3-й строк также равны нулю, так как 1-я и 2-я строки одинаковы. Поскольку все миноры третьего порядка равны нулю, то все миноры высших порядков также равны нулю. Таким образом, ранг матрицы равен 2, так как порядок максимального ненулевого минора равен 2.

Ранг матрицы можно найти с помощью элементарных преобразований матрицы не меняющих ее ранга. К таким преобразованиям относятся:

1. перестановка двух строк (столбцов);

2. умножение строки (столбца) на некоторое число ;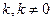

3. прибавление к одной строке (столбцу) другой, умноженной на какое-либо число k, не равное нулю;

4. исключение из матрицы строки (столбца), состоящей из нулей;

5. исключение из матрицы строки (столбца), являющейся линейной комбинацией других строк (столбцов)

Пример 2. Применяя элементарные преобразования, найти ранг матрицы

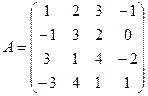
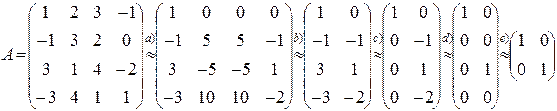
Опишем произведенные элементарные преобразования матрицы:

a) 1-й столбец прибавим к 4-му, а затем, последовательно умножая его на (-2) и (-3), прибавим соответственно ко 2-му и 3-му столбцам.

b) Исключим 2-й и 3-й столбцы, так как они получаются из 4-го столбца умножением на (-5). Уже на этом шаге очевидно, что ранг получившейся матрицы равен 2, так как существует ненулевой минор равный 2. Это минор, состоящий из первых двух строк.

Преобразование матрицы тем не менее можно продолжить

c) Сначала 1-ю строку прибавим ко 2-й, а затем последовательно умножив на (-3) и 3, прибавим соответственно к 3-й и 4-й строкам.

d) Сначала 3-ю строку прибавим ко 2-й, а затем, умножив ее на 2 прибавим к 4-й строке.

e) Исключим нулевые строки. Определитель последней матрицы не равен нулю. Строки ее линейно независимы. Таким образом, ранг этой матрицы равен двум.

Все вышеизложенные понятия необходимы для решения вопроса о совместности системы линейных уравнений. Пусть дана система линейных уравнений:

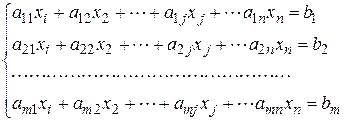(1)