Упражнения. где а – некоторый числовой параметр

1. Решить систему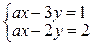

где а – некоторый числовой параметр. Указать, при каких значениях а система: а) имеет единственное решение; б) не имеет решений; в) имеет бесчисленное множество решений.

Ответ: а) При 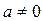система имеет единственное решение ( 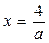; 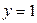); б) при 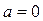система не имеет решений; в) бесчисленного количества решений система ни при каких значениях а иметь не может.

2. Методом Гаусса решить систему

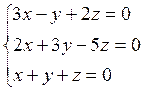
Ответ: система имеет лишь тривиальное решение ( ; ; ).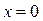

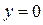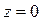3. Показать, что переопределенная система

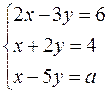
может иметь решение. При каком значении параметра а это будет иметь место?

Ответ: при 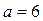система имеет единственное решение ( 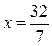; 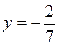). При 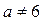система не имеет решений.

4. Решить недоопределенную систему

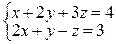
Ответ: система имеет бесчисленное множество решений

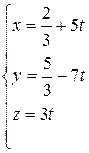(t – свободный параметр)

5. Решить недоопределенную систему

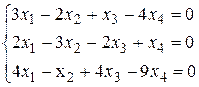
Ответ: система имеет бесчисленное множество решений

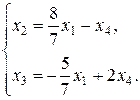(x₁,x₂– свободные параметры)

6. Методом Гаусса решить систему: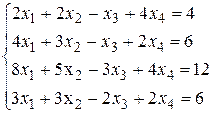

Ответ: (1,1,-1,-1).