Базис пространства.

Линейно независимая система векторов, через которые линейно выражается каждый вектор пространства, называется базисом пространства. Пусть 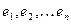базис этого пространства, так как всякий вектор 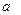пространства 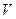одно однозначно представляется в виде линейной комбинации векторов 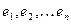, то ввиду (1) образ вектора 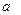с теми же коэффициентами выражается через образы векторов 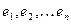, т.е. всякое линейное преобразование 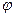пространства 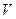однозначно определяется заданием образов 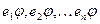. Из координат образов мы можем составить матрицу А. Строками этой матрицы будут координаты образов базисных векторов. Покажем, что образ любого вектора х мы можем получить умножив матрицу А на х. Возьмем произвольный вектор х, 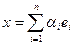. В силу (1) 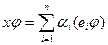, что равносильно матричному равенству 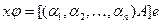. Другими словами, строка координат вектора 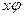равна строке координат вектора х, умноженной справа на матрицу А линейного преобразования 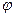, все в базисе е: .

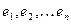Линейное преобразование полностью характеризуется его матрицей. Поэтому действия над такими преобразованиями сводятся к действиям над их матрицами.

Нахождение собственных чисел (характеристических корней ) и собственных векторов квадратных матриц.

Пусть 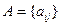- квадратная матрица порядка n c действительными элементами, Х – вектор-столбец, 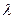- некоторое неизвестное. Умножим матрицу А на вектор Х . Произведение будет вектором-столбцом, элементы которого обозначим через 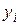.Если окажется, что элементы 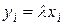(i=1,2 … n), т.е. пропорциональны соответствующим элементам вектора-столбца х с коэффициентом пропорциональности 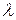, то вектор-столбец х называется собственным вектором матрицы А, а коэффициент пропорциональности 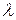- характеристическим числом матрицы А, или её собственным значением. Другими словами, вектор х называется собственным вектором матрицы А, а число 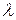- её характеристическим числом , или её собственным значением, если выполняется равенство 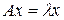. Перепишем это уравнение в виде 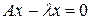или

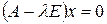(2)

где Е - единичная матрица, порядок которой равен порядку матрицы А, а 0 – нулевой вектор-столбец, т.е. столбец все элементы которого равны нулю. Матрица 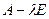называется характеристической матрицей матрицы А . Так как в матрице 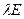по главной диагонали стоит 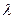, а все остальные элементы равны нулю, то

.

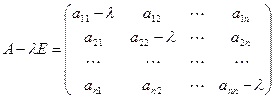При условии, что вектор 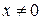, равенство (2) возможно только тогда, когда определитель его левой части равен нулю, т.е. 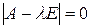. Это уравнение называется характеристическим уравнением матрицы А. Оно также носит название векового уравнения, потому что к нему приводит в небесной механике задача исследования вековых возмущений планет.

Определитель матрицы 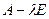будет многочленом от 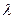степени n. Этот многочлен называется характеристическим многочленом матрицы А. Характеристическое уравнение запишется так:

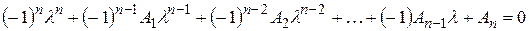, где

А₁ – сумма всех диагональных миноров 1- го порядка;

А₂ – сумма всех диагональных миноров 2- го порядка;

……………………………………………

А_n – сумма всех диагональных миноров n- го порядка.

Этот способ составления характеристического уравнения носит еще название метода непосредственного развертывания.

Его корни 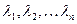, среди которых могут быть равные, называются характеристическими корнями матрицы А или ее собственными значениями. Они могут быть как действительными, так и комплексными. Весь набор характеристических корней, причем каждый корень берется с той кратностью, какую он имеет в характеристическом многочлене, называется спектром линейного преобразования .

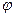Каждому собственному значению матрицы А на основании уравнения 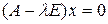, или, что то же самое: 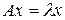, соответствует собственный вектор.

Собственным вектором матрицы А, принадлежащим собственному значению 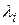, называется ненулевой вектор, для которого столбец х, составленный из его элементов, удовлетворяет матричному уравнению 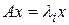. Любой собственный вектор можно определить с точностью до постоянного множителя. Подставляя в (2) поочередно все собственные значения 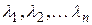, получим n собственных векторов.

Собственные числа и собственные вектора матрицы А имеют большое значение в описании линейного преобразования, задаваемого этой матрицей. Собственные вектора определяют направление (прямую), которая остается неизменной при данном линейном преобразовании. Собственные значения определяют коэффициент пропорциональности векторов и их образов на этом неизменном направлении.

Пример 1.Найти собственные числа и собственные вектора матрицы :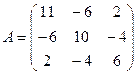

Решение.

Составим характеристическое уравнение и найдем собственные значения матрицы:

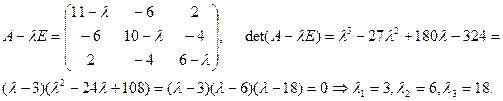
Поставим в уравнение 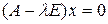поочередно все собственные значения и найдем координаты собственных векторов.

Составим систему для нахождения первого собственного вектора. После подстановки в (2) первого собственного значения мы имеем:

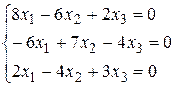
Определитель этой системы равен нулю. Здесь независимы только два уравнения ( действительно, если сложить второе уравнение в третьим и сумму умножить на –2, то получится первое уравнение ). Рассмотрим систему, состоящую из первого и второго уравнений :

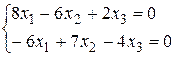
Пусть 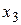- свободная неизвестная. Пусть 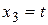, тогда

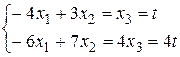
Решим эту систему по методу Крамера :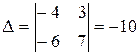

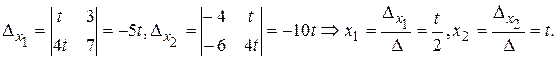
таким образом, первый собственный вектор имеет координаты:

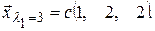
Аналогично, из системы: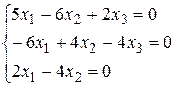

где независимых уравнений только два ( если второе уравнение разделить на –2 и сложить с третьим, то получится первое ) мы получим систему, состоящую из второго и третьего уравнения. Решив ее, получим второй собственный вектор:

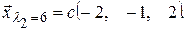
Составим систему для третьего вектора:

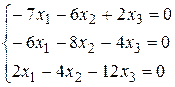
Здесь опять-таки только два уравнения независимы (если первое уравнение умножить на –2, а второе на 2 и сложить их, то получится третье уравнение). Получилась система, содержащая два первых уравнения. Решив ее, получим третий собственный вектор: .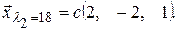

Ответ. , ,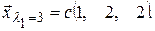

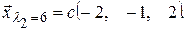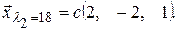
Пример 2.Найти собственные числа и собственные вектора матрицы : .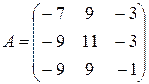

Решение.

Собственные числа матрицы А найдем из характеристического уравнения матрицы. Согласно методу непосредственного развертывания для матрицы третьего порядка это уравнение имеет вид: ,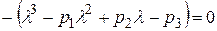

где 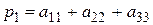, ( сумма диагональных элементов матрицы ),

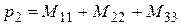, ( сумма диагональных миноров второго порядка )

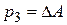, ( определитель матрицы ).

Вычислив указанные коэффициенты, составим уравнение: 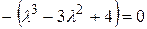. Корни этого уравнения являются собственными числами: 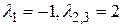.Первое число соответственно кратности 1, а второе – кратности 2. Для нахождения собственных векторов подставим найденные значения в уравнение: .

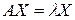Для 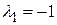получим систему: 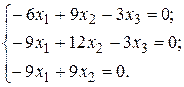Из последнего уравнения следует, что 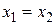. Используя это равенство в первом уравнении, получим, что 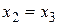. Таким образом, 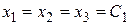, где С₁ – любое число. Итак, первый собственный вектор: .

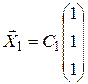Найдем собственный вектор, соответствующий кратному собственному числу 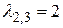. Для него получаем систему:

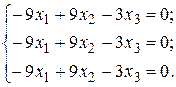
Фактически, это одно уравнение 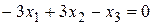, полагая 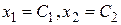, можем записать: 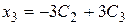, тогда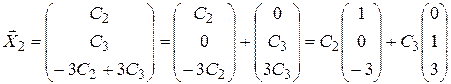

Ответ. , .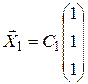

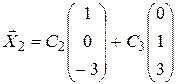Пример 3.Рассмотрим модель автопарка. Предположим, что автомобили могут использоваться на протяжении одного года, двух или трех лет. Допустим, что 100% автомобилей, срок службы которых три года, заменяются новыми, парк машин, прослуживших два года, обновляется лишь на 20%; все машины со сроком службы в один год продолжают эксплуатироваться на протяжении следующего года.

Тогда число машин, используемых первый год, определяется 100%-ным обновлением тех автомобилей, у которых не позднее, чем год назад истек трехлетний срок службы, и 20%-ным обновлением парка тех машин, у которых не позднее чем год назад истек двухлетний срок службы. Число машин, используемых второй год, совпадает с числом автомобилей, у которых не позднее чем год назад истек одногодичный срок службы. Наконец, автомобили, используемые на протяжении третьего года, составляют 80% парка машин, у которых не позднее, чем год назад истек двухлетний срок службы.

Формализуем задачу, представив распределение машин по годам в виде векторов: 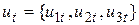, где индекс t обозначает номер года, а элементы 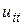- число автомобилей, которые к началу t-го года уже прослужили i лет. Вектора могут быть объединены в матрицу 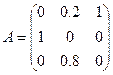. С помощью этой матрицы может быть осуществлена связь между векторами распределения машин по срокам службы в (t-1) и t годах : 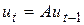. Кроме того, эта модель позволяет ответить на вопрос: может ли существовать при данных условиях не изменяющееся во времени распределение машин по срокам службы. Другими словами, требуется найти собственный вектор матрицы А для собственного значения .

Сначала удостоверимся, что 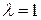действительно является собственным значением матрицы А. Составим характеристическое уравнение.

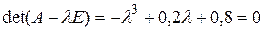
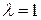действительно является корнем этого уравнения. Вычислим собственный вектор, соответствующий этому собственному значению, согласно описанной выше процедуре. Получится вектор 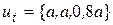. Поскольку этот вектор является собственным для собственного значения 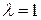, то он не будет меняться год от года. Это означает, что парк автомобилей, внутри которого число машин, служащих первый год, совпадает с числом машин, служащих второй год, а количество машин, служащих третий год, составляет 80% этой величины, будет все время сохранять стабильную структуру.