Дадим определение линейного пространства.
Лекция 8. Линейное преобразование вектора, запись в матричном виде. Собственные числа и собственные векторы матрицы, характеристическое уравнение. Решение характеристического уравнения. Нахождение собственных векторов в случае различных и кратных корней. Метод итераций для определения наибольшего собственного числа.
Линейные пространства.
Дадим определение линейного пространства.
Пусть дано множество 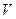 ; его элементы будут обозначаться малыми латинскими буквами:
; его элементы будут обозначаться малыми латинскими буквами: 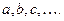 Пусть во множестве
Пусть во множестве 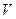 определены операция сложения, ставящая в соответствие всякой паре элементов
определены операция сложения, ставящая в соответствие всякой паре элементов 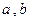 из
из 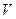 однозначно определенный элемент
однозначно определенный элемент 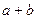 из
из 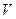 , называемый их суммой, и операция умножения на действительное число, причем произведение
, называемый их суммой, и операция умножения на действительное число, причем произведение 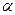
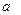 элемента
элемента 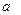 на число
на число 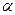 однозначно определено и принадлежит к
однозначно определено и принадлежит к 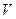 . Элементы множества
. Элементы множества 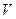 будут называться векторами, а само
будут называться векторами, а само 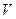 – действительным линейным пространством, если указанные операции обладают следующими свойствами:
– действительным линейным пространством, если указанные операции обладают следующими свойствами:
1. Сложение коммутативно, 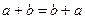 .
.
2. Сложение ассоциативно, 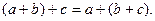
3. В V существует нулевой элемент 0, удовлетворяющий условию: 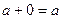 для всех
для всех 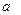 из
из 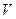 .
.
4. Для всякого элемента 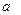 в
в 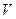 существует противоположный элемент -
существует противоположный элемент - 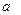 , удовлетворяющий условию:
, удовлетворяющий условию: 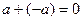 .
.
Дальнейшие аксиомы связывают умножение на число со сложением и с операциями над числами. Именно, для любых элементов 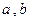 из
из 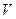 , для любых действительных чисел
, для любых действительных чисел 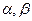 и для действительного числа 1 должны иметь место равенства.
и для действительного числа 1 должны иметь место равенства.
5. 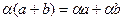
6. 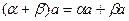
7. 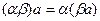
8. 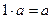
Дата добавления: 2015-10-05; просмотров: 762;
