Линейные преобразования линейного пространства.

Если задано правило, по которому каждому элементу (вектору) 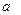линейного пространства поставлен в соответствие элемент (вектор) 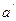того же пространства, то говорят, что задано преобразование этого пространства. Элемент 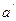называется образом элемента 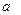при рассматриваемом преобразовании. Если преобразование обозначено через 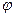, то образ вектора 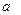будем обозначать 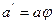. Преобразования также называются операторами.

Преобразование 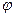называется линейным, если сумму любых двух векторов 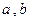оно переводит в сумму образов этих векторов

,

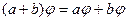а произведение любого вектора 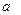на любое число 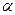переводит в произведение образа вектора 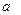на это же число .

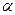Из этого определения немедленно вытекает, что линейное преобразование линейного пространства переводит любую линейную комбинацию данных векторов 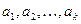в линейную комбинацию ( с теми же коэффициентами ) образов этих векторов.

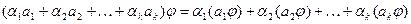(1)