Аффинные преобразования
Аффинным называется преобразование, обладающее следующими свойствами:
● любое аффинное преобразование может быть представлено как последовательность операций из числа простейших: сдвиг, растяжение/сжатие, поворот;
● сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.
Аффинные преобразования координат на плоскости:
(x, y) – двумерная система координат,
(X, Y) – координаты старой СК в новой системе координат.
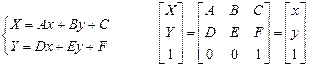 |
Общий вид аффинного преобразования:
A, B, C, D, E, F – константы.
Обратное преобразование также является аффинным:
Простейшие аффинные преобразования системы координат.
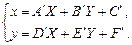 |
1.
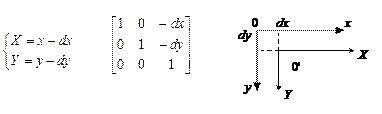 |
Параллельный сдвиг координат:
 |
Обратное преобразование:
2. Растяжение/сжатие осей:
Обратное преобразование
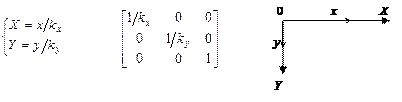 |
:
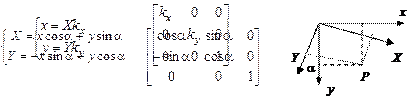 |
Коэффициенты могут быть отрицательными. Например, при kx = -1 получаем зеркальное отображение относительно оси y.
3. Поворот системы координат (x,y) на угол α:
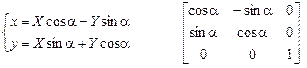 |
Обратное преобразование – поворот системы (X,Y) на угол (-α):
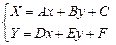 |
Аффинные преобразования объектов на плоскости.
x, y – старые координаты точки, X, Y – новые координаты точки.
1.
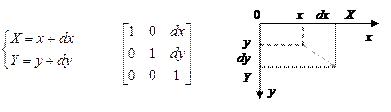 |
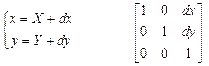
Сдвиг:
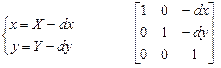 |
Обратное преобразование:
2.
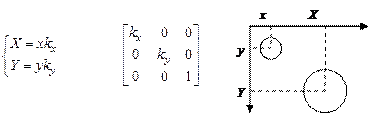 |
Масштабирование объекта:
Обратное преобразование:
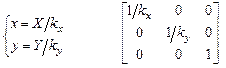 |
3. Поворот вокруг центра координат:
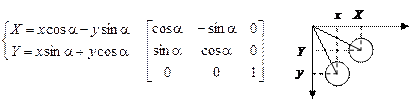 |
Обратное преобразование:
Дата добавления: 2015-11-20; просмотров: 2355;
