Кривые второго порядка
Общий вид уравнения линии 2-го порядка:
a1x2+a2y2+a3xy+a4x+a5y+a6=0.
Рассмотрим различные формы линий 2-го порядка.
Уравнение окружности:
(x-x0)2+(y-y0)2=r2 – нормальное уравнение окружности,
C(x0, y0) – центр окружности,
M(x,y) – произвольная точка окружности,
x2+y2+ax+by+g=0,
a=-2x0;b=-2y0; g=x02+y02-r2.
Ax2+Ay2+Dx+Ey+F=0– общее уравнение окружности.
Действительная окружность при (a2+b2)/4-g³0, где a=D/A; b=E/A; g=F/A.
Таким образом, действительная кривая 2-го порядка является окружностью тогда и только тогда, когда:
1) коэффициенты при квадратах текущих координат равны между собой;
2) отсутствует член, содержащий произведение текущих координат.
Центральные кривые 2-го порядка – кривые, имеющие собственный центр симметрии.
A(x-x0)2+C(y-y0)2=D, A¹C.
O(x0, y0) – центр симметрии кривой;
x=x0, y=y0 – оси симметрии кривой.
Пусть x0=0 и y0=0.
Кривая 2-го порядка принадлежит эллиптическому типу, если коэффициенты A и C имеют одинаковые знаки, т.е. AC>0.
Пусть A>0 и C>0, тогда если:
● D>0 – действительный эллипс, x2/a2+y2/b2=1–каноническое уравнение эллипса;
● D=0 – вырожденный эллипс (кривая вырождается в точку);
● D<0 – мнимый эллипс.
Кривая 2-го порядка является кривой гиперболического типа, если коэффициенты A и C имеют противоположные знаки, т.е. AC<0.
Пусть A>0, тогда C<0:
● если D>0 – гипербола (рис. 7), x2/a2-y2/b2=1–каноническое уравнение гиперболы;
● если D=0 – вырожденная гипербола представляет собой пару пересекающихся прямых
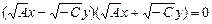 ;
;
 |
● если D<0 – сопряженная гипербола (рис. 7), xy=a2 (a>0) – обратная пропорциональность. Графиком является равнобочная гипербола (к уравнению гиперболы легко прийти, повернув оси координат на 45 º – рис. 8).
 |
Нецентральные кривые 2-го порядка не имеют центра симметрии или имеют бесконечное множество центров, могут иметь ось симметрии.
(y-y0)2=2p(x-x0) – парабола, O(x0, y0) – вершина параболы,
P – параметр параболы.
Если вершина параболы находится в начале координат и p>0, то y2=2px – каноническое уравнение параболы.
Дата добавления: 2015-11-20; просмотров: 2423;
