Взаимное расположение графических элементов на плоскости
1. Три точки p1, p2, p3 коллинеарны, т.е. лежат на одной прямой, если
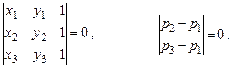 |
2. Точка p лежит на отрезке ab при нулевом угле между векторами p-a и b-p:
(p - a) ◦ (b - p)= |p - a|·|b - p| ,
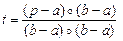 .
.
Взаимное расположение прямых.
1. Две прямые совпадают, если F1× F2 =03 (векторное произведение равно нулевому вектору).
2. Две прямые параллельны, если
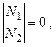
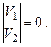
3. Две прямые ортогональны, если N1◦ N2=0 или V1◦ V2=0.
Взаимное расположение точки и прямой
1. Уравнение перпендикуляра, опущенного из точки
q=[qx, qy] на прямую, выглядит следующим образом:
(НФ): Ny(x-qx)-Nx(y-qy)=0,
(ПФ): p┴(t)=q+Nt или p┴(t)=q+V┴t , где V┴=[Vy, -Vx]=N.
2. Расстояние от точки q до прямой равно:
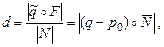
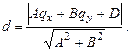
3. Зеркальное отражение точки q относительно прямой лежит на перпендикуляре к прямой на расстоянии 2d от q в сторону, противоположную проекции вектора q-p0 на нормаль N:
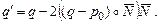
Пересечение двух прямых.
Пусть имеются две прямые, заданные уравнениями в НФ:
A1x+B1y+D1=0 и A2x+B2y+D2=0,
тогда координаты точки пересечения вычисляются следующим образом:
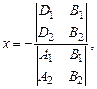
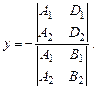
Возможны следующие три случая:
1. A1B2-A2B1≠0, т.е. A1/A2≠B1/B2 – прямые не параллельны, точка пересечения единственная и ее координаты вычисляются по вышеприведенным формулам.
2. A1B2-A2B1=0, D1B2-D2B1≠0 или A1D2-A2D1≠0 – прямые параллельны и точек пересечения нет.
3. A1B2-A2B1=0, D1B2-D2B1=0 и A1D2-A2D1=0, т.е. прямые совпадают во всех точках.
Угол между двумя пересекающимися прямыми находится как угол между векторами нормали или направляющими векторами Ð(N1, N2) = Ð(V1, V2).
Дата добавления: 2015-11-20; просмотров: 1825;
