III. Виды понятий, выделяемые по характеру элементов объема.

а) Собирательные и разделительные.

Практически это самое важное различение видов понятий, нотому что с выделением этих видов непосредственно связаны способы действий с понятиями. Эти виды понятий относятся только к общим понятиям. Единичные (и, конечно, пустые) понятия не могут быть ни разделительными, ни собирательными.

Элементы объема понятия могут быть двух видов: 1) они могут быть единичными объектами, 2) они сами могут быть множествами объектов. В связи с таким разделением выделяются два вида понятий:

Собирательным называется понятие, элементы объема которого сами составляют множества однородных объектов.

Пример. К числу собирательных понятий относятся: «толпа», поскольку элементами объема понятия «толпа» являются отдельные толпы, которые, в свою очередь, состоят из однородных предметов — людей; «библиотека» — поскольку элементы объема этобо понятия являются отдельные библиотеки, которые, в свою очередь, состоят из однородных предметов — книг; парламент, коллектив, созвездие, флот и т.п.

Разделительным называется понятие, элементы объема которых не представляют собой множеств однородных обшектов.

Пример. Большинство понятий являются разделительными. Человек, студент, стул, преступление – разделительные понятия.

Главная особенность способа обращения с разделительными и собирательными понятиями состоит в том, что с ними следует обращаться одинаково. Смысл нашего различения состоит в том, чтобы всегда отдавать себе отчет, что на самом деле является элементом объема собирательных понятий, а что – разделительных понятий. В понятии «библиотека» элементом объема понятия служат не книги, а библиотеки. Если говорят, что библиотеку затопило, это не означает, что каждая книга погибла в воде. Элементом объема понятия «общественный класс» являются не отдельные люди — буржуа, крестьяне или рабочие, а большие группы людей. И поэтому если вам говорят, что нечто в интересах такого-то класса, то это не означает, что это в интересах каждого рабочего, буржуа, крестьянина. Из того, что полк разбит, не следует, что убит каждый солдат или офицер. Нужно также отдавать себе отчет, что считать частью объема таких понэтий. Например, часть объема понятия «университет» — это то или иное множество университетов, а не те или иные факультеты данного университета. Здесь следует помнить о проведенном ранее различении отношения рода и вида и отношения части и целого.

Однако трсдности с феноменом «собирательности» на этом не заканчиваются. Дело в том, что многие понятия могут употребляться как в разделительном, так и в собирательном смысле. «Граждане нашего государства поддерживают идею частной собственности» не означает, что каддый гражданин государства поддерживает эту идею. По мнению автора такого высказывания, граждане нашего государства в целом поддерживают эту идею. Здесь понятие «граждане нашего государства» используется в собирательном смысле. «Граждане нашего государства обязаны соблюдать закон» — в этом высказывании речь идет о каждом гражданине, т.е. понятие «граждане» употребляется здесь в разделительном смысле.

б) Абстрактные и конкретные.

Это деление понятий на виды важнее всего философски. Мы уже рассматривали слоао «абстракция» и установили, что оно происходит от латинского слова, имеющего значение «отвлекать». Что и от чего мы отвлекаем в акте абстракции? Ответ на этот вопрос подсказывает наша онтология. В мире существуют предметы, у которых есть свойства и между которыми имеются отношения. В акте абстракции мы отвлекаем, отделяем свойство от предмета или отношение от предметов, которым они присущи. Рассмотрение свойств и отношений самих по себе, независимо от тех предметов, которым они принадлежат или которые они связывают, является характерной чертой абстрактного мышления. Любое мышление, которое претендует на общность своих выводов, является абстрактным. Если мы высказываем некоторые верные суждения относительно свойств или отношений самих по себе, независимо от объектов, которым они принадлежат или которые они связывают, то мы высказываем верные суждения для всех этих объектов. Поэтому научное мышление всегда является абстрактным.

Такое понимание абстракции помогает нам понять, что же имеется в виду под абстракрными и конкретными понятиями.

Абстрактными называются понятия, элементами объема которых являются свойства или отношения.

Иначе говоря, в этих понятиях выделяются и обобщаются не предметы, а их свойства или отношения.

Пример. «Справедливость», «белизна», «преступность», «осторожность», «присущность», «отцовство» и т.п. — все это абстрактные понятия.

Конкретным называется понятие, элементами объема которого являются предметы.

Пример. «Стул», «стол», «преступление», «тень», «музыка» — все это конкретные пмнятия.

В абстрактных понятиях свойства и отношения не превращаются в предметы. Они рассматриваются как объекты (см. главу 3, § 1), что дает нам возможность составлять из них множества и рассматривать их как элементы множеств, составляющих объемы понятий. Мы помним, что, описывая нашу логическую онтологию, мы разделили свойства и отношения, с одной стороны, и предметы — с другой. Это разделение помогает нам четко мыслить два различных вида понятий: абстрактные и конкретные.

Иногда, исходя из конкретных понэтий, образуют связанные с ними абстрактные понятия. Например, на основе понятия «человек» можно образовать понятие «человечность», элементом объема которого будет сложное свойство «быть человеком». На основе такой операции знаменитый древнегреческий филосмф Платон конструировал такие понятия, как «стульность», «лошадность», которые он называет идеями и которые, по его мнению, служат прообразами вещей чувственного мира. По Платону, чувственные вещи даны нашим чувствам, а такие понятия, как «стульность», «лошадность» и т.п. — только зрению нашего ума[14].

Прием мышления, при помощи которого абстрактным понятиям придается самостоятельное, независимое от предметов существование, называется гипостазированием.

Поэтому мы можем сказать, что Платон гипостазировал абстрактные понятия: «благо», «истина», «добро», «красота» и т. п. Правильно ли он это сделал или нет, уже не дело логики, этот вопрос рассматривают философы.

Большинство абстрактных понятий, типа понятий «справедливость», «истинность», «равенство», «братстао» и т.п., являются единичными понятиями; поскольку бывает только одно свойство человеческих поступков «быть справедливым», одно свойство суждений «быть истинным», одно отношение между людьми «быть равным» или «быть братом». Понятие «справедливость» всегда является единичным понятием, независимо от того, совершаются справедливые поступки или нет, и много ли их совершается, поскольку свойство такое все равно существует и при том только одно.

Некоторые абстрактные понятия бывают все же общими. Рассмотрим понятие «цвет». Элементами объема этого понятия служат такие свойства: желтый, синий, красный и т.п., т.е. некоторые простые свойства предметов. Следовательно, понятие может быть абстрактным, но в то же время и общим, поскольку в объеме его содержится более мдного элемента.

Примеры абстрактных понятий, которые мы рассматривали выше, показывают, что среди абстрактных понятий встречаются такие понятия как «справедливость», «истина», «красота», «добро», «равенство» и т. п. Такие понятия в философии, психологии, социологии называются ценностями. Это наводит нас на мысль, что теория абстрактных понятий может быть использована для определения понятия «ценность».

Чтобы дать определение ценности, попытаемся выяснить основные признаки этого понятия: 1) ценности принимаются/отвергаются сознательно, 2) ценности говорят о свойствах или отношениях объектов, 3) ценности объявляют объекты, обладающие указанным в ценности свойством положительно значимыми, а не обладающими отрицательно значимыми (в другой интерпретации также и безразличными). Отсюда получается определение ценности:

Ценность - это абстрактное понятие, разделяющее область объектов, к которой оно применяется, на два класса - положительно значимых и отрицательно значимых объектов.

Пример. «Истина» – это абстрактное понятие, в котором обобщается и выделяется свойство суждений «быть истинным». Как ценность истинность придает суждениям, обладающим этим свойством («истинным суждениям») положительное значение, а не обладающим этим свойством («ложным суждениям») – отрицательное значение.

Пример. «Красота» – абстрактное понятие, в объеме которого содержится свойство «быть красивым». Соответственно, ценность «красота» придает объектам, обладающим этим свойством, положительное значение, а не обладающим им – отрицательное еначение[15].

На данных примерах видно, как теория понятия применяется для того, чтобы дать ясную и отчетливую трактовку одного из важнейших понятий гуманитарного знания.

§ 2. Отношения между понятиями

Ав: Здравствуйте, друзья! Подумайте над следующей задачей: кого в мире больше — отцов, сыновей или мужчин?

Сс: Конечно, мужчин.

Ав: А потом?

Сс: Ну, наверное, отцов, а потом сыновей. Хотя с сыновьями и отцами не очень ясно.

Ст. Подождите, мы же уже умеем изображать объемы понятий при помощи кругов Эйлера. (Подходит к доске и рисует следующую картинку:

Рис. 1

Получится вот так! Здорово, взяли и нарисовали мысли!

Сс: Ты уверен, что это правильно?

Ст: Ты сам так сказал.

Сс: Я-то сказал… Но правильно ли я сказал?

Ав: Да, это очень хороший вопрос. Давайте посмотрим. (Обращается к рисунку Студента-тугодума). Рассмотрим какой-нибудь предмет, который входит в объем понятия «отец», но не входит в объем понятия «сын», как нарисовано на вашей картинке. (Подходит к доске и ставит точку в круге «отцы» следующим образом:

Рис. 2

Что же получается? У вас существуют отцы, которые не являются сыновьями. Это хорошо?

Ст: Нет, этого не может быть.

Сс: Да, но то же самое можно сказать и о понятиях «сын» и «мужчина». У нас получилось, что не каждый мужчина — сын.

Ав: Придется нам в этом деле разобраться.

Наше рассмотрение объемов понятий и множеств показывает, что один и тот же объект может быть элементом объема различных понятий. Так, Иван Петрович Сидоров одновременно может быть элементом объемов понятий «человек», «студент», «мужчина», «спортсмен», «избиратель» и т.п. Уже этот простой факт показывает, что данные понятия вступают между собой в определенные отношения, поскольку имеют общий элемент. Но ведь a priori[16] можно предположить, что в определенные отношения вступают и те понятия, которые не имеют общих элементов — ведь это уже само по себе определенное отношение.

Рассмотрим произвольную пару понятий A и B.

Понятия A и B назовем сравнимыми, если в содержаниях этих понятий имеется хотя бы один общий признак.

Пример. Понятия «мужчина» и «женщина» сравнимы, поскольку в их содержаниях есть общий признак «быть человеком».

Почти все понятия сравнимы. Даже божий дар и яичница в нашей логической онтологии являются предметами, а следовательно, имеют в своем содержании общий признак. Обратите внимание, что в этом определении речь идет не об основном содержании, а обо всем содержании понятия. Поэтому почти у каждой пары понятий можно найти общий признак.

Понятия A и B назовем несравнимыми, если в содержаниях этих понятий не встречается ни одного общего признака.

Мы не будем иметь дела с несравнимыми понятиями, поэтому не будем их подробно рассматривать.

До сих пор речь шла о содержании понятий. Содержание представляет собой сложный признак, в котором могут встречаться много простых признаков, соединенных различным образом (через «и», «или» и т.п.). Поэтому с рассмотрением соотношения понятий по содержанию возникают сложности. Чтобы избежать неточностей, можно было бы ограничиться основным содержанием понятий, как оно определено в § 2 этой главы. Для этого надо в определениях заменить слово «содержание» на слово «основное содержание». Однако надо иметь в виду, что в таком случае сравнимость и несравнимость понятий будет зависеть от того, каким образом мы сформулируем основное содержание понятий.

Более точной является теория отношений понятий по объему.

Рассмотрим пару сравнимых понятий A и B.

Понятия A и B назовем совместимыми, если объемы этих понятий имеют хотя бы один общий элемент

Пример. Понятия «футболист» и «гений» совместимы, потому что существуют гениальные футболисты, например, Эдуард Стрельцов или Пеле.

Понятия A и B назовем несовместимыми, если в объемах этих понятий нет ни одного общего элемента.

Пример. Понятия «божий дар» и «яичница», как предполагается в поговорке «спутал божий дар с яичницей», несовместимы, т. е. ни один объект по имени «божий дар» не является в то же время объектом по имени «яичница». Короче говоря, эта поговорка гласит, что ни одна яичница не является божьим даром и наоборот.

Если обозначить объем понятия тем же символом, что и само понятие, то условие совместимости двух понятий можно записать так:

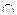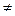А В Æ,

а условие несовместимости так:

А В=Æ.

В отличие от сравнимости-несравнимости понятий нас будут интересовать как виды совместимости, так и виды несовместимости понятий.

Виды совместимости

Представим себе возможные случаи совместимости двух понятий A и B. Во-первых, может быть так, что объемы понятий A и B совпадают. Во-вторых, может быть так, что объем понятия B целиком входит в объем A, но в то же время имеются такие элементы A, которые не являются элементами объема понятия B. В-третьих, может быть так, что объемы понятий имеют общую часть, но есть такие элементы объема понятия B, которые не являьтся элементами объема понятия A и наоборот.

Рассмотрим эти три случая подробнее.

Понятия A и B назовем равнозначными, если объемы этих понятий состоят из одних и тех же элементов.

Отношения между понятиями по объему удобно иллюстрировать кругами Эйлера. В данном случае получится следующий рисунок:

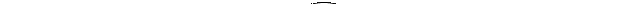
Рис. 3

Пример. Следующие понятия являются равнозначными: (A) Луна и (B) естественный спутник Земли; (A) квадрат и (B) равносторонний прямоугольник; (A) дочь и (B) женщина; (A) сын и (B) мужчина; (A) сын и (B) внук.

Понятие B подчиняется понятию A, если объем B является собственным подмножеством объема A.

Несложно заметить, что вид понятия подчиняется самому этому понятию, а любое понятие подчиняется своему роду.

При помощи кругов Эйлера это отношение изобразим таким образом:

Рис. 4

Пример: Следующие понятия находятся в отношении подчинения: (B) студент и (A) человек; (B) человек и (A) животное; (B) историк и (A) гуманитарий; (B) мать и (A) дочь — все это пары понятий, из которых первое подчиняетсэ второму.

Понятия A и B находятся в отношении перекрещивания, если они совместимы и имеются элементы объема понятия A, не являющиеся элементами объема понятия B, и элементы объема понятия B, не являющиеся элементами объема понятия A.

При помощи кругов Эйлера отношение перекрещивания можно изобразить следующим образом:

Рис. 5

Пример. (A) студент и (B) спортсмен, (A) женщина и (B) красивый человек, (A) монархия и (B) демократическое государство — все это пары перекрещивающихся понятий.

Как устанмвить, в каком отношении находятся совместимые понятия? Для этого следует задать нашим понятиям A и B два вопроса:

1. Все ли A являются B?

2. Все ли B являются A?

Если мы на оба вопроса отвечаем «да», то получаем отношение равнозначности.

Если мы на первый вопрос отвечаем «да», а на второй — «нет», то понятие A подчиняется понятию B.

Если мы на первый вопрос отвечаем «нет», а на второй — «да», то понятие B подчиняется понятию A.

Если мы на оба вопроса отвечаем «нет», то получаем отношение перекрещивания,

Пример. Рассмотрим понятия «сын» и «мужчина». Причем под мужчиной будем понимать человека мужского пола. Зададим наши вопросы.

Все ли сыновья являются мужчинами? — Да.

Все ли мужчины являются сыновьями? — Да.

Следовательно, мы получили отношение равнозначности.

Пример. Теперь рассмотрим отношения между понятиями «сын» и «отец».

Всякий ли сын является отцом? — Нет.

Всякий ли отец является сыном? — Да.

Мы получили отношение подчинения, причем понятие «отец» подчиняется понятию «сын»[17].

Это дает нам решение задачи, приведенной в диалоге наших персонажей в начале этого параграфа. Графически это решение можно представить следующим образом:

Рис. 6

Если подытожить наше рассмотрение видов отношения совместимости, то мы получим следующую диаграмму:

Рис. 7