Но в силу только что доказанной теоремы

,

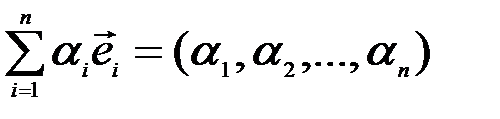а последний вектор является нулевым лишь при условии 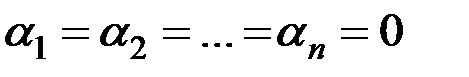. Во-вторых, всякий вектор 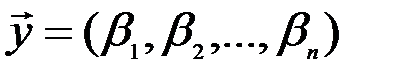заведомо представим в виде линейной комбинации векторов 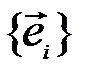: 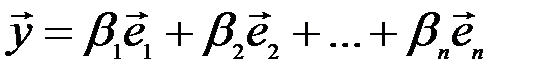и, значит, набор 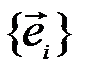образует базис.

Векторное пространство 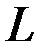называется 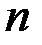-мерным, если в нем существуют 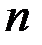линейно независимых векторов, а любые 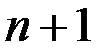векторов уже являются линейно зависимыми. При этом число 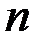называется размерностьюпространства .

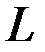Размерность векторного пространства, состоящего из одного нулевого вектора, принимается равной нулю. Размерность пространства 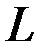обычно обозначают символом .

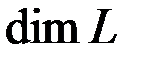Векторное пространство 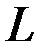называется бесконечномерным, если в нем существует любое число линейно независимых векторов. В этом случае пишут .

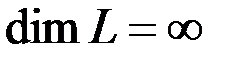Выясним связь между понятиями базиса и размерности пространства.

Теорема 3.7. Если 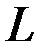– векторное пространство размерности 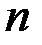, то любые 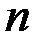линейно независимых векторов этого пространства образуют его базис.

Доказательство. Пусть 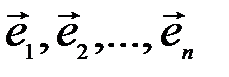– произвольная система 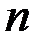линейно независимых векторов пространства 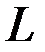(существование хотя бы одной такой системы следует из определения 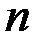-мерного пространства). Если 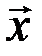– любой вектор пространства 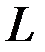, то согласно определению система из 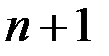векторов 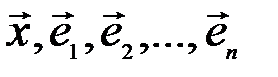линейно зависима, т.е. найдутся не все равные нулю числа 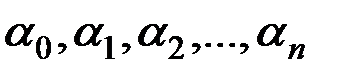такие, что справедливо равенство

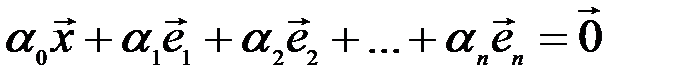. (3.9)

Заметим, что число 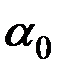заведомо отлично от нуля (ибо в противном случае из равенства (3.9) вытекала бы линейная зависимость векторов 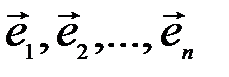). Но тогда, деля равенство (3.9) на 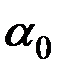и полагая

,

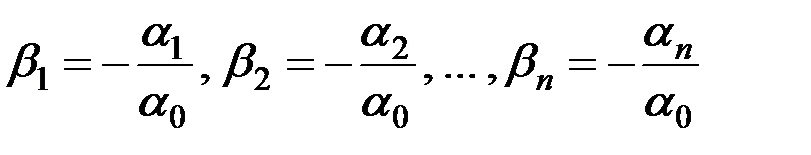получаем из (3.9)

.

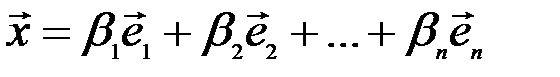Так как 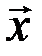– произвольный элемент из 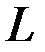, то последнее равенство доказывает, что система векторов 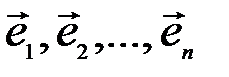является базисом пространства .

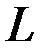Теорема 3.8. Если векторное пространство 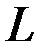имеет базис, состоящий из 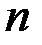векторов, то 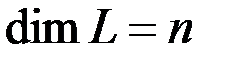. (Без доказательства)