Алгебра множеств. Ее формулы, теоремы и законы

В математике алгеброй называют множество объектов с введенными на них операциями.

Определение. Алгеброй множеств называют совокупность множеств и операций над ними — предметных (È, Ç , \, D, Ø) и сравнения (Í , Ì , = ), а также отрицаний операций сравнения.

Определение. Формулой алгебры множеств называют любое выражение вида А r В, где А, В — формулы множеств, r — операция сравнения либо ее отрицание.

Формулы, справедливые для любых входящих в них множеств, называются теоремами алгебры множеств. Они задают всегда верные рассуждения о множествах. Количество всех возможных теорем алгебры множеств бесконечно.

Пример 1. Рассмотрим следующие выражения:

а) Ø (АÈВ) = Ø А ØВ; б) АÈВ = АÇВ;

в) АÇВ Í АÈВ; г)(АÈВ) Ç С = (АÇC) È (BÇС).

Выражение а) не является формулой алгебры множеств, так как в правой части его стоит выражение, не являющееся формулой множества. Выражения б) и в) — формулы алгебры множеств. Как нетрудно показать на примерах, равенство б) справедливо только в одном случае, когда А = В, в других случаях оно ложно. Поэтому оно не будет теоремой. Нестрогое включение в) и равенство г) выполняются всегда, поэтому они являются теоремами алгебры множеств.

Среди теорем особо выделяют такие, где используется операция сравнения «равенство» ( = ), поскольку такие теоремы задают эквивалентные преобразования формул (не нарушающие их истинности). Наиболее употребительные теоремы с равенствами называют законами алгебры множеств. В качестве законов обычно приводят следующие теоремы:

1. Коммутативные законы — действуют относительно операций объединения и пересечения.

АÈВ =ВÈА; АÇВ =ВÇА.

2. Ассоциативность (для операций объединения и пересечения).

(АÈВ)ÈС =АÈ(ВÈС) =АÈВÈС);

(АÇВ)ÇС =А Ç(ВÇС) =А ÇВÇС.

3. Дистрибутивные законы.

(АÈВ)ÇС =(АÇC)È(BÇС);

(АÇВ)ÈС=(АÈC)Ç(BÈС).

4. Идемпотентность.

АÈА =А ; АÇА =А.

5. Поглощение.

АÈ(АÈВ)= АÈВ; АÇ(АÇВ) =АÇВ.

6. Законы де Моргана.

Ø(АÈВ)= Ø АÇ ØВ; Ø (АÇВ)= Ø АÈ ØВ.

7. Закон исключения третьего.

Ø Ø А = А.

8. Операции с пустым и универсальным множествами.

(АÈU)=U; (АÈÆ) =A;

(АÇU)=A; (АÇÆ)= Æ;

(UÇÆ)=Æ; (UÈÆ)= U;

Ø Æ =U; Ø U =Æ .

Рассмотрим проверку правильности рассуждений о множествах, задаваемых формулами алгебры множеств. В общем случае она может быть выполнена с использованием полных диаграмм пересечений, а также с помощью векторов включений.

Пример 2. Проверить справедливость первого закона де Моргана: Ø (АÈВ) = Ø А Ç ØВ.

Решение. Необходимо выяснить равенство в общем случае составныхмножеств, заданных формулами F₁ = Ø (АÈВ)и F₂ = Ø А Ç ØВ. Построим на полных множествах элементарных пересечений векторы включения для F₁ и F₂:

Так как данные векторы совпадают, то составные множества, заданные формулами F₁ и F₂, равны при любых входящих в них множествах А и В. Рассмотренное равенство является теоремой алгебры множеств.

Также строгое доказательство закона можно дать на полной диаграмме пересечений для двух множеств (рис.1.2).

Для доказательства того, что некоторая формула не является теоремой алгебры множеств, достаточно указать хотя бы один случай её нарушения — например, на конкретных множествах или на диаграммах Венна, которые не обязательно должны быть полными диаграммами пересечений.

Пример 3. Будет ли теоремой формула А\В = Ø(АÇВ)?

Решение. Проверка на диаграмме Венна для произвольных множеств U, A, B (рис. 1.3) показывает, что формула дала неверный результат, следовательно, она не будет теоремой.

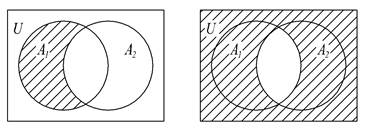
Рис.1.3

Замечание Доказанный выше факт не означает, что конкретные составные множества, задаваемые формулами Ø(АÇВ)и А\В, всегда не равны. Например, в частном случае при A=U равенство выполняется, поскольку А\В= ØВ, Ø(АÇВ)= ØВ.

ЗАДАЧИ

1. Выразить аналитически в виде формул множества а)—ж) (рис.1.4), указанные на диаграммах Венна штриховкой:

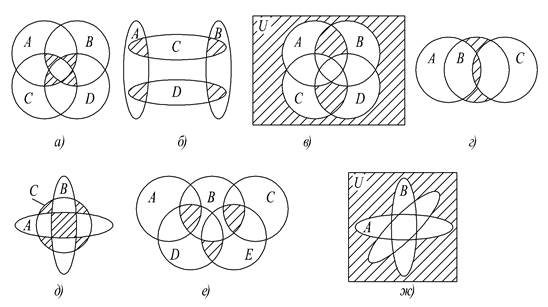
Рис. 1.4.

2. Изобразить, используя полные диаграммы пересечений Венна, множества, заданные формулами:

а) (АDВ) È (СDВ), б) А Ç(ВÈС), в) ØАÇВ, г) Ø (Ø(А\В)\С), д) Ø (Ø АD В), е) Ø ( А \ Ø В), ж) Ø (Ø ( АÇВ)\ С), з) Ø А D(СÈØ В) , и) (АDØВ) Ç(ØВÈ С).

3. Сравнить следующие пары составныхмножеств, заданные формулами:

а) Ø (АÈВ) и ØА Ç Ø B, б) (АÇВ) Ç (AÈC)и (BÇA) Ç (BÈC), в) (A\B) D ØB и Ø А Ç Ø B, г) АÈB и (А\B)D B, д) (ADB)\С и (А\(BÈC)) È(В\ (AÈC)).

4. Проверить (доказать или опровергнуть), будут ли приведенные ниже формулы теоремами алгебры множеств:

а)(ADB) È Ø (AÈВ) =Ø( АÇВ), б) АÇ(В\A) = Æ , в) А\(ВÈС) = АÇØ (ВÈС), г) (AÈB)Ç A = A, д) (A DB)\С = (А\(BÈC)) È (В\ (AÈC)), е) ØA D ØB Í АÈB , ж) А\(BÈC) Í Ø В, з) АÇВ Í (AÈB) D C, и) АDВ Í Ø(AÇBÇC).