Мощность. Счетные множества

Количество элементов конечных множеств может быть выражено неотрицательным целым числом. Для оценки количества элементов в бесконечных множествах вводится обобщенное понятие числа — мощность, которая для конкретного множества А обозначается как ÷ А÷. На конечных множествах она совпадает с числом элементов, ее можно определить простым подсчетом.

Пример 1. |{a,b,c}|=3; |{1,...,10}|=10.

Для исследования мощности бесконечных множеств используют отображения.

Определение. Множества А и В называют эквивалентными (имеющими одинаковую мощность), если между ними можно установить взаимно однозначное отображение. Обозначают как: | А|=| В|.

Для конечных множеств эквивалентность означает равенство чисел элементов.

Рассмотрим самый простой вид бесконечных множеств.

Определение. Cчетными называют все множества, эквивалентные множеству N натуральных чисел. Мощность ôNô обозначают À₀ (алеф нуль, алеф – первая буква древнееврейского алфавита):ôNô = À₀.

Основное свойство счетных множеств заключается в том, что их элементы можно пронумеровать числами натурального ряда. Это позволяет использовать различные алгоритмы их последовательной обработки.

Вопрос о допустимости использования в математике бесконечных величин и множеств занимал умы мыслителей еще с древности. Уже тогда признавалось существование потенциальной бесконечности, под которой понимается отсутствие предела у возрастающих числовых последовательностей, например у натурального ряда N.

В то же время, многие видные ученые, начиная с античности (Аристотель) до второй половины XIX века (Лейбниц, Гаусс, Коши и др.), выступали против признания и использования в математике актуальной бесконечности, при которой бесконечные множества в символьном виде вводятся в формулы, подобно обычным конечным, и с ними допускается выполнение различных действий.

Переворот совершил в конце XIX века немецкий математик Георг Кантор, который вопреки существовавшему мнению, ввел в математику актуально-бесконечные множества, доказав целый ряд теорем, раскрывающих их свойства.

Пример 2. Найдем мощность множества N₂ всех четных положительных чисел (делящихся без остатка на 2).

Решение. Все числа в N₂ имеют вид: n₂=2n, где nÎN. Отображение f:N®N₂, задаваемое этой зависимостью, является линейным с ненулевым линейным коэффициентом (С₀=2). Как доказано ранее, оно взаимно однозначно. По определению множества N₂и N эквивалентны.Таким образом, множество N₂ так же счетно, как и N, ôN₂ô =ôNô= À₀.

Пример 3. Найти мощность множества Z всех целых чисел
в интервале (– ¥; + ¥).

Решение. Аналогично доказываем ïZï=À₀ путем построения взаимно однозначного отображения f : Z® N. Разобьем Z на два подмножества: N, N_- , где N_- — неположительные целые числа (0 и все отрицательные). Обозначим через N₂ множество натуральных четных чисел, через 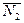— множество натуральных нечетных чисел ({1,3,5,7,...}).

Искомое отображение f строим из двух отдельных взаимно однозначных отображений следующим образом:

N® N₂; n₂= 2n;

N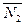_- ® ; n_`2= –2n_-+1.

И первая и вторая части построенного отображения являются линейными с ненулевыми линейными коэффициентами (С₀=2,
–2),следовательно, они взаимно однозначны. Так как
Z = NÈN_-; N=N₂ È 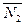, то искомое взаимно однозначное отображение построено. Следовательно, ïZï=ôNô =À₀.

Замечание. Взаимно однозначное отображение может быть построено различными способами. В примере 3 его можно указать, например, следующим образом:

A: 0 1 2 –1 –2 3 4...

¯ ¯ ¯ ¯ ¯ ¯ ¯ ...

N: 1 2 3 4 5 6 7 ...

Пример 4. Найти мощность множества A рациональных чисел в сегменте [0,1].

Решение. По определению рациональными являются числа, которые могут быть представлены в виде a = ± n / m, где n, m — целые числа, n ≥ 0, m > 0. На сегменте [0,1] n £ m. Упорядочить данные числа можно следующим образом. В первой строке расположить числа, где после сокращения числителя и знаменателя знаменатель равен 1; во второй — несократимые числа со знаменателем 2, не вошедшие в строку 1; в третьей — несократимые числа со знаменателем 3,не вошедшие в строки 1 и 2, и т.д.

В итоге получаем таблицу:

m=1: 0/1, 1/1;

m=2: 1/2;

m=3: 1/3,2/3;

m=4: 1/4, 3/4;

...

Таблица содержит все числа из А, причем каждое входит ровно один раз. Если задать порядок по строкам таблицы сверху вниз и внутри строк слева направо, то каждому ее элементу можно взаимно однозначно поставить в соответствие свой порядковый номер — натуральное число:

0/1 « 1, 1/1 « 2, 1/2«3, 1/3«4, 2/3«5, 1/4«6, 3/4«7,…

Отсюда следует, что построено взаимно однозначное отображение f : A®N ,ïAï = À₀ .

Пример 5. Найти мощность множества A рациональных чисел на всей числовой оси (–¥; +¥).

Решение. Рациональные числа в А можно представить в виде a = ± n / m, где n, m — целые неотрицательные числа (m ¹ 0). Упорядочиваем их аналогично рациональным числам из [0,1], рассматривая вместо знаменателей веса чисел W = n + m. Таблица будет иметь вид:

W=1: 0/1;

W=2: +1/1; –1/1;

W=3: +2/1; +1/2; –1/2; –2/1;

...

Вводя пересчет элементов по аналогии с примером 4, также можно показать, что в данном случае ïAï = À₀.

Для практического определения счетноймощности множеств можно использовать следующие утверждения.

Теорема 2.1. Любое подмножество B счётного множества А конечно или счётно.

Доказательство. Упорядочим элементы множества А = {a₁, a₂, …} и удалим из него все элементы, не входящие в В. При этом всегда будет получено упорядоченное конечное или бесконечное (счетное) множество элементов, составляющее подмножество B.

Теорема 2.2. Объединение любого конечного или счётного числа счетных множеств тоже всегда является счётным множеством.

Доказательство. Допустим, есть конечное или счётное число множеств А₁, А₂, А₃,... .Объединение их обозначим через А. В общем случае А₁, А₂, А₃, ... могут пересекаться, поэтому перейдем к непересекающимся множествам В₁ = А₁; В₂ = (A₂ \ A₁); В₃ = (A₃ \ (A₁ È A₂))и т. д. Очевидно, È B_i = = È A_i = A. Мощность числа элементов в каждом множестве B_i не превышает счётную. Поэтому их можно записать в виде упорядоченной последовательности (b_i1, b_i2, ...).Объединяя такие записи множеств B₁,B₂,..., получим запись элементов всего исходного множества А в виде таблицы:

b₁₁ b₁₂ b₁₃ ...

b₂₁ b₂₂ b₂₃ ...

b₃₁ b₃₂ b₃₃ ...

...

В этой таблице все элементы А присутствуют ровно один раз. Для доказательства счетности множества А графически укажем на рис.2.1 способ упорядочения его элементов (сопоставления их числам из натурального ряда).

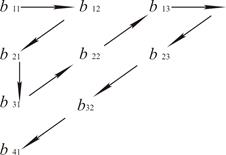
Рис. 2.1

Данный способ упорядочения задает взаимно однозначное отображение множества А на N. Отсюда следует: ïAï=À₀.

Пример 6. На плоскости (x, y) задана ортогональная сетка с шагом 1 (рис.2.2). Найти мощность множества А узлов сетки.

Решение. Мощность множества горизонтальных линий равна мощности множества всех целых чисел Z. Выше показано, что оно счетно. Также счетно множество вертикальных линий. По доказанной ранее теореме о счетной сумме счетных множеств получим: |А| = À₀.

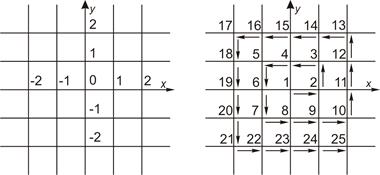
Рис. 2.2 Рис. 2.3

Замечание. Задачу можно решить, непосредственно указав взаимно однозначное отображение f: A® N. Например, так, как показано на рис. 2.3.

Для практического сравнения мощностей множеств также может быть использована теорема, сформулированная Кантором и доказанная Шредером и Бернштейном.

Теорема 2.3. Кантора-Бернштейна. Пусть А и В — некоторые произвольные множества. Если А эквивалентно некоторому подмножеству В₁ множества В, а В — некоторому подмножеству А₁ из А, то А эквивалентно В:ôАô=ôВô.

Доказательство производится путем построения взаимно однозначного отображения между А и В.