Пример 1. 1. АÈВÇС — формула множества, которую с учетом введенного старшинства операций следует понимать как АÈ(ВÇС).
1. АÈВÇС — формула множества, которую с учетом введенного старшинства операций следует понимать как АÈ(ВÇС).
2. С Ø А — запись не является формулой множества, так как в ней одноместная операция дополнения соединяет два множества.
Для наиболее полной характеристики содержательного смысла формулы составного множества F, в которую входят простые множества А1, А2,…, Аn, рассмотрим множество {R} всех возможных пересечений простых множеств либо их дополнений {А1a1Ç А2a2Ç…Ç Аn an}, где ai = 0или1, Аi1= Аi, Аi0= ØАi. Представляя вектор индексов (a1,a2,…,an) в виде записи двоичного числа N в промежутке от 0 до 2n–1, упорядочиваем по возрастанию этих чисел все элементы {R}. Назовем их элементарными пересечениями. Эти пересечения для двух и трех простых круговых множеств даны в виде диаграмм Венна на рис. 1.2.
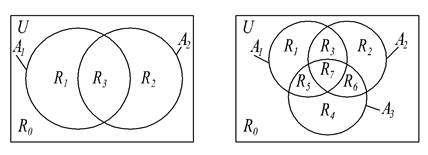
Рис.1.2
Диаграммы Венна для заданного числа исходных множеств, на которых показаны все их возможные элементарные пересечения, назовем полными диаграммами пересечений. Такие диаграммы с круговыми изображениями исходных множеств могут быть построены только для двух и трех множеств (рис.1.2). При четырех и выше необходимо использовать вместо кругов более сложные фигуры.
Таблицы с упорядоченными по возрастанию чисел N элементарными пересечениями для двух и трех простых множеств имеют вид:
| N | А2 | А1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 1 | 0 |
| 3 | 1 | 1 |
| N | А3 | А2 | А1 |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 |
Любой формуле составного множества F(А1, А2,…, Аn) можно взаимно однозначно поставить в соответствие вектор, отражающий вхождение в него элементарных пересечений {R}. Назовем его вектором включений. Если формула имеет сложный вид, построение данного вектора можно проводить поэтапно. При объединении двух множеств в итоговом векторе включений учитываются единицы из обоих векторов, при пересечении остаются только единицы, входящие одновременно в оба вектора. При применении отрицания в векторе происходит замена 0 на 1 и 1 на 0. При вычитании А\В в итоговый вектор включают 1 только в том случае, когда в векторе А стоит 1, а векторе В — 0.
Пример 2.Построить векторы включений для составных множеств, заданных на простых множествах А и В следующими формулами: 1) F1 = Ø (АÈВ), 2) F2 = Ø(АDВ), 3) F3 = АÇВ È Ø(АÈВ). Результаты привести в таблице.
Решение. При определении векторов включений используем старшинство операций. Вектор для F1 строим поэтапно, используя объединение АÈВ. Вектор включений для F2 находим с использованием формулы АDВ =( А\В) È (В\А) . В случае F3 рассматриваем предварительно векторы формул АÇВ, АÈВ и Ø (АÈВ).
| N | А | В | АÈ В | F1 | АD В | F2 | АÇ В | Ø (АÈ В) | F3 |
Данную конструкцию назовем таблицей пересечений.
ЗАДАЧИ
1. Определить, будут ли следующие выражения формулами множеств:
а) АÇС\; б)Ø А È Ø В; в) Ø (Ø АDC); г) Ç С?
2. Указать очередность выполнения операций в формулах:
а) Ø А D Ø ВÈС; б) Ø А ÇØ С; в) АÈВÇСÈD.
3. Построить таблицы пересечений и изобразить все элементарные пересечения на полных диаграммах пересечений для составных множеств, заданных формулами:
а) (АDВ)\С; б) Ø(АÈВÈС) ; в) АÇ (В È С) ; г) (АDВ) È (А\Ø С) ; д) АÇ ВÇ СÈ(ВD ØС).
4. Привести примеры непустых исходных множеств А, В, С, при которых будет выполняться равенство составных множеств:
а) АDВ и АÈВ; б) А \ ( ВÈС) и А\В.
1.6. Операции сравнения — логические операции
с множествами
Определение. Два множества А и В называют равными, если они состоят из одних и тех же элементов. Обозначается равенство как А=В.
Если все элементы множества А принадлежат множеству В
("а Î А Þ а Î В), то говорят, что А нестрого включается в В. Обозначают как А Í В.
Если АÍВ, но А¹В, то имеет место строгое включение, которое обозначают как АÌ В.
Операции равенства нестрогого и строгого включений (=; Í; Ì) называют операциями сравнения.
Дата добавления: 2015-10-05; просмотров: 1223;
