Предметные операции на множествах. Формула множества

Для того чтобы можно было конструировать множества сложной структуры (составные) из некоторых исходных (простых), на них вводятся предметные операции. Рассмотрим их.

Определение. Объединением множеств А и В называют множество С, содержащее элементы, входящие хотя бы в одно из них. Обозначают как С = АÈВ ={x | (xÎA)или(xÎB)}.

Пересечением множеств А и В называют множество С, содержащее элементы, входящие одновременно в А и В. Обозначают: С = АÇВ ={x | (xÎA)и(xÎB)}.

Разностью множеств А и В называют множество С, содержащее все элементы из множества А, не входящие в В. Обозначают: С = А\В ={x | (xÎA), но (xÏB)}.

Симметрической разностью множеств А и В называют множество С, содержащее элементы из А\В и из В\А. Обозначают: С = АDВ =(А\В) È(В\А) .

Рассмотрим множества, состоящие из объектов некоторого вида, содержащихся в заданном универсальном множестве U. Дополнением множества А называют множество С, содержащее элементы из U, не входящие в А. Обозначают дополнение: С=`А либо С = Ø А.

Дополнение любого множества можно представить как результат его вычитания из универсального: Ø А = U \ А.

Результатом выполнения рассмотренных предметных операций (È, Ç, \, D, Ø)всегда является множество.

Определение. Формулой множества называется:

1) любое выражение вида А, В, С,…, где А, В, С,…— обозначения простых множеств, заданных непосредственным определением;

2) любое выражение вида АÈВ; АÇВ; А\В; АDВ; Ø А, где
А, В — формулы множеств.

Графически множества изображают в виде плоских фигур (кругов, овалов и т.д.). Такие изображения называют диаграммами Венна. На диаграммах а) — д) рис.1.1 показаны результаты выполнения введенных выше операций объединения, пересечения, разности, симметрической разности и дополнения.

Для упрощения записи выражений, содержащих операции на множествах, обычно принимают, что самой сильной операцией (выполняющейся ранее других, если другой порядок не оговорен скобками) является отрицание. Второй по силе операцией является пересечение, остальные — равносильны. Если операции равны по силе, то они выполняются в порядке слева направо.

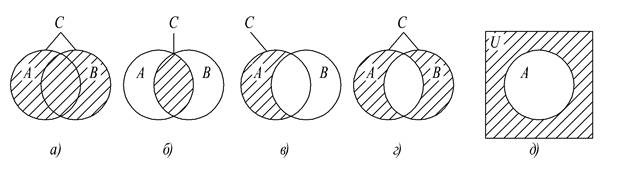Рис.1.1