Отображения, функции, предикаты

Определение. Рассмотрим множества А и В. Отображением f множества А в множество В называют любое правило, по которому элементам аÎА ставятся в соответствие элементы bÎB. При этом элемент bÎB называют образом элемента аÎА, а элемент а называют прообразом элемента b.

При обозначении отображений используют префиксную форму, где их знак ставится в начале записи. Для конкретных элементов обозначение имеет вид: f(а)= b, для множеств А и В: f : А ® В.

Определение. Для отображения f: А ® В множество А называют областью определения отображения f, множество В — областью значений. Множество образов b = f(а)всех элементов области определения А называют образом множества А и обозначают f(А).

Определение. Если областью определения отображения является декартово произведение длины n: f: А₁ ´ А₂ ´…´ А_n ® В, то отображение называют n-местным.

Определение. Отображение f: А ® В называют инъекцией, если образы любых двух различных элементов а₁ÎА, а₂ÎА, а₁¹ а₂тоже различны: f(а₁) ¹ f(а₂), т.е. в инъекции различные элементы из области определения не могут отображаться в один образ.

Отображение f: А ® В называют сюръекцией, если f(А)= В, т. е. образом области определения А является вся область значений В.

Отображение f: А ® В, являющееся одновременно инъекцией и сюръекцией, называют взаимно однозначным или биекцией.

Важный практический смысл биекции или взаимно однозначного отображения f: А ® В заключается в том, что каждому элементу аÎА ставится в соответствие один и только один образ f(а) = bÎВ, и наоборот, каждому образу bÎВ соответствует один и только один прообраз аÎА. При этом общее количество элементов в конечных множествах А и В совпадает. Проверить взаимную однозначность (биективность) отображения можно
и другим путем.

Определение. Отображение f: А ® В называют однозначным, если любому элементу аÎА поставлен в соответствие единственный элемент bÎB.

Определение. Пусть f — отображение из А в В (f: A ® B). Обратным к f называется отображение f^–1: B ® A, которое переводит элементы bÎB в элементы аÎА, такие, что f(a)=b.

Утверждение. Если отображение f: A® B однозначно и обратное к нему отображение f ^–1: B ® A существует и однозначно, то f является биекцией (взаимно однозначным отображением).

Пример 1. Пусть A = {места в вагоне}, B = {пассажиры}, отображение f задано билетами. В вагоне есть свободные места. Здесь отображение f: A ® B инъективно, но не сюръективно (f однозначно, но обратное отображение f ^–1: B ® A не определено на свободных местах). Поэтому f не взаимно однозначно.

Пример 2. Пусть A = {места в вагоне}, B = {пассажиры}, отображение f задано билетами. В вагоне все места заняты. Здесь отображение f: A ® B взаимно однозначно, поскольку оно одновременно инъективно и сюръективно (f однозначно, обратное к нему отображение f ^–1: B ® A существует и также однозначно, а именно, каждому месту соответствует пассажир).

Определение. Пусть на множествах А, В, С заданы отображения g: A ® B; f: В ® С. Композицией отображений g и f называют отображение h = fg (h: A ® C), полученное при последовательном применении отображений g и f.

Операция композиции сохраняет взаимную однозначность отображений, т. е., если g и f взаимно однозначны, то h = gf также представляет собой взаимно однозначное отображение.

Отображения f: A ® B, где областью значений B являются числовые множества, называют функциями.

Для них используют ту же систему обозначений, что и для отображений. Различие в терминологии следующее.

Определение. Пусть f — функция, действующая из области определения А в область значений В: f: A® B. Элементы аÎА называют аргументами функции f, элементы b = f(a)ÎB — значениями функции f.

Для функций, как для частного случая отображений, также рассматривают инъективность, сюръективность, биективность, однозначность и обратные функции.

Пример 3. А = R — множество всех вещественных чисел, B =[–1,+1], f = sin. Функция f однозначна, но не взаимно однозначна, так как значения образов b = sin(a) по заданному элементу аÎА определяются однозначно, а обратное отображение f ^–1: B ® A, задающее значения прообразов по их образам (a = sin^–1(b)), имеет при каждом b бесконечное число решений (функция сюръективна, но не инъективна).

Пример 4. A =[ –p¤2, p¤2]; B =[–1,+1]; f = sin. Данная функция взаимно однозначна.

Пример 5. Рассмотрим произвольную линейную функцию f с ненулевым линейным коэффициентом, отображающую одно множество вещественных чисел A на другое — B . В общем случае формула перехода от элемента aÎA к некоторому элементу bÎB имеет вид: b = С₀a + С₁, где С₀и С₁— некоторые константы. При С₀¹ 0 такая функция однозначна.

Докажем от противного. Допустим, существует некоторый элемент a¢ÎA, который отображается на множество B не единственным образом, т.е. имеет как минимум два различных образа b¢ и b¢¢ (b¢–b¢¢¹ 0). Так как b¢ = С₀ a¢ + С₁ и b¢¢ = С₀ a¢ + С₁, то, вычитая из первой формулы вторую, получим: b¢–b¢¢ = С₀(а¢––а¢)= 0. При С₀¹0 это противоречит предположению
о различии b¢ и b¢¢, а следовательно, о неоднозначности рассмотренной линейной функции.

Следствие. Любая линейная функция f с ненулевым линейным коэффициентом не только однозначна, но и взаимно однозначна.

Справедливость данного утверждения следует из того, что обратной к линейной функции f, переводящей элементы aÎA в элементы bÎВ по формуле b = С₀ a + С₁ (где С₀¹ 0), будет также линейная функция f ^-1с ненулевым линейным коэффициентом, переводящая элементы bÎВ в элементы aÎA по формуле a =(1/С₀) b – С₁/С₀.

Особое место среди отображений занимают логические функции, называемые также предикатами.

Определение. Отображение называют логической функцией или предикатом, если ее областью значений являются логические значения «ложь» («false») и «истина» («true»), которые в математике обозначают соответственно 0 и 1. Таким образом, у логической функции область значений Е₂ = {0,1}.

Предикаты, как и отображения, могут быть n-местными. В отличие от отображений и функций их обозначают заглавными латинскими буквами с индексами и без — например, Q(x), Р(х,у), R₂(x,y,z). Поскольку результат у предикатов — логическое значение, то они формулируются в отличие от обычных числовых функций в виде некоторого логического условия.

Определение. Областью истинности предиката Р(х₁, х₂, …, х_n), определенного на декартовом произведении Х₁´Х₂´…´Х_n, называется множество наборов значений (х₁, х₂, …, х_n), принадлежащих Х₁´Х₂´…´Х_n , на которых Р(х₁, х₂, …, х_n)= «истина» (Р(х₁, х₂, …, х_n) = 1).

Пример 6. U = R. Q(x)= «x больше 0». Для любого вещественного числа x можно определить, положительно оно или нет. В первом случае Q(x)=1 , во втором Q(x)=0. Областью истинности данного предиката будет множество R⁺,входящее в U = R .

Пример 7. U =`R⁺. Q₁(x) = «x может быть представлен в виде дроби m/n, где m и n — целые числа, m ≥ 0, n >0 ». Поскольку логическое условие предиката совпадает с определением неотрицательного рационального числа, то его областью истинности будут все такие числа на неотрицательной числовой полуоси.

Пример 8. U = R². Р(x,у) = «x больше у». Областью истинности предиката Р(x,у)на декартовой плоскости Оxу будет полуплоскость, лежащая ниже прямой х = у.

Функции, у которых область значений В совпадает с областью определения А, называют предметными.

Определение. Пусть множество А задано на некотором более широком множестве В. Характеристической функцией множества А называется функция c_А(х), определенная на В, такая, что

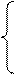c_А(х)= 0, если хÏА,

1, если хÎА.

Характеристическую функцию можно интерпретировать как предикат, если придать числовым значениям 0 и 1 логические значения «ложь» и «истина».