Булевы функции, способы их задания. Элементарные функции. Алгебра логики, ее формулы
Определение. Пусть`хn ― n-мерный двоичный вектор. Функция f(`хn),`х n Î E2n, принимающая значения 0 и 1, называется булевой функцией или функцией алгебры логики.
По числу переменных n функции алгебры логики называют одноместными ( n = 1), двухместными ( n = 2 ) и т.д.
Способы представления функций алгебры логики f (хn)зависят от представления всех наборов значений E2n, которые принимает вектор её переменных`хn . Наиболее просто все возможные наборы можно перечислить в таблице, где они располагаются в лексикографическом порядке по возрастанию соответствующих им двоичных чисел. Значения истинности функции f помещаются в отдельном столбце, который называется вектором истинности функции f (хn). Вся конструкция называется таблицей истинности функции f (х n).
Рассмотрим элементарные функции, которые являются базовыми в алгебре логики.
1. Константы. Функции, определенные при любом числе переменных n и принимающие на всех наборах только одно значение истинности (0 или 1 ).
2. Одноместные функции, не являющиеся константами. Обозначив переменную в них через х, получим следующие таблицы истинности:
| х | F1 | f2 |
Определение. Функцию f1 называют тождественной. Обозначают: f1(х)= х. Функцию f2называют отрицанием. Обозначают: f2(х) = Ø х либо f2(х) =`х.
3. Двуместные функции. Рассмотрим следующие двуместные функции, не являющиеся константами и которые нельзя свести к одноместным функциям. Переменные обозначим через х и у:
| x | y | f3 | f4 | f5 | f6 | f7 | f8 | f9 |
Определение. Функцию f3называют конъюнкцией (логическим умножением). Способы обозначения следующие: f3(х, у)= х & у , либо f3(х, у) = ху , либо f3(х, у) = х Ù у.
Функцию f4называют дизъюнкцией (логическим сложением). Обозначают: f4(х, у) = х Ú у .
Функцию f5называют сложением по модулю 2. Обозначают: f5(х, у) = х Å у .
Функцию f6называют эквивалентностью. Обозначают как: f6(х, у)= х º у либо f6(х, у) = х « у.
Функцию f1называют импликацией. Обозначают: f1(х, у)= х® у либо х É у.
Функцию f8называют штрих Шеффера. Обозначают: f8(х, у)= х| у .
Функцию f9называют функцией Вебба или стрелкой Пирса. Обозначают: f9(х, у) = х ¯ у .
Определение. Символы Ø , &, Ú, Å, º, ®, |, ¯ ― называют логическими связками.
Для упрощения записи выражений приняты следующие соглашения о силе логических связок:
1) Ø― самая сильная (при отсутствии скобок применяется ранее других),
2) & ― вторая по силе,
3) связки Ú, Å, ®,|,¯равносильны,
4) связка ºсамая слабая.
Равносильные связки выполняются в порядке слева направо.
Функции 0, 1, f1– f9 называют элементарными. При помощи этих функций можно выразить более сложные n-местные функции алгебры логики (n ³3).
Определение. Соседними по переменной хi называют пары булевых векторов`a=(a1..., ai-1, 0, ai+1,..., an)и`b=(a1,..., ai-1, 1,ai+1, ...,an), различающиеся только по одной переменной хi. Существенными называются такие переменные хi функции f(хn), для которых существует хотя бы одна пара соседних по хi наборов значений переменных`aи`b, на которой f(a)¹ f(b). Если же изменение только одной переменной не влечет изменение функции, то эта переменная называется фиктивной.
Фиктивные переменные могут быть исключены из формульного выражения функции. Очевидно, у констант все переменные являются фиктивными, у функций f1― f9 ― все переменные являются существенными.
Пример 1. Найти существенные и фиктивные переменные функции трех переменных f(х, у, z), таблица истинности которой приведена ниже.
| х | у | z | f |
Решение.
1. На наборах (0, 0, 0), (1, 0, 0), соседних по х, f(0, 0, 0)¹ f(1, 0, 0), следовательно, переменная х ― существенная.
2. Так как на всех парах наборов, соседних по у ― (0, 0, 0) и (0, 1, 0), (0, 0, 1)и (0, 1, 1), (1, 0, 0)и (1, 1, 0), (1, 0, 1)и (1, 1, 1)―функция принимает одинаковые значения, то у ― фиктивная переменная.
3. На наборах (0, 0, 0), (0, 0, 1), различающихся только значениями переменной z, f(0, 0, 0) ¹ f(0, 0, 1), следовательно, переменная z ― существенная.
Ответ: переменные х, z ― существенные, у ― фиктивная.
Для функции из примера 1 можно предложить формулу f(х, у, z) = x Å`z, в которую не входит фиктивная переменная у.
Наряду с элементарными, выделим и другие наиболее употребительные типы булевых функций.
Определение. Элементарными пороговыми называют функции одной и двух переменных, у которых значение истинности изменяется один раз ― либо на нулевом наборе переменных (0, 0,..., 0) либо на единичном наборе (1, 1,..., 1).
Данные функции имеют очевидный логический смысл и простую физическую реализацию. К пороговым относятся обе одноместные функции, существенно зависящие от своей переменной ― тождественная функция f1(х) = х и отрицание f2(х) =`х. Среди двуместных функций пороговыми являются 4 функции: 1) конъюнкция f3 = &, 2) дизъюнкция f4= Ú, 3) штрих Шеффера f8=| , 4) функция Вебба f9 =¯.
Пороговый (скачкообразный) принцип действия рассмотренных двухместных функций f3, f4, f8 , f9позволяет ввести их аналоги на случай произвольных n - местных функций.
Определение. Обобщенными пороговыми называют следующие n - местные функции:
1) обобщенная конъюнкция &(х n), равная 1 при`х n = (1, 1, ..., 1)и 0 на всех остальных наборах,
2) обобщенная дизъюнкция Ú (х n), равная 0 при `х n = (0, 0, ..., 0)и 1 на всех остальных наборах,
3) обобщенная функция Шеффера | (`х n), равная 0 при `х n = (1, 1, ... , 1) и 1 на всех остальных наборах,
4) обобщенная функция Вебба ¯ (`х n), равная 1 при `х n =(0, 0, ... , 0)и 0 на всех остальных наборах.
Принципиальная схема функционального элемента, реализующего обобщенную конъюнкцию &(хn), может быть представлена (рис.2.1 а) в виде последовательного соединения входов 1,...,n, соответствующих переменным (х1,..., хn). Сигнал от входа В к выходу&схемы передается только при одновременной подаче дополнительных сигналов на все входы 1,...,n. В противном случае цепь разрывается. Схема обобщенной дизъюнкции Ú(`хn), может быть представлена (рис.1.1 б) в виде параллельного соединения входов 1,...,n. В ней для появления выходного сигнала достаточно его подачи хотя бы на один из входов.
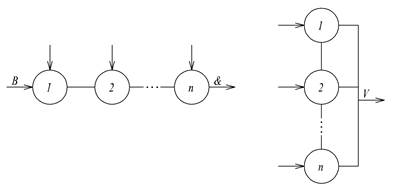
а) б)
Рис.1.1
Применяя дополнительно отрицание к входам схемы, аналогично можно представить обобщенные функции Вебба (Рис.1.2 а) и Шеффера (Рис 1.2 б).
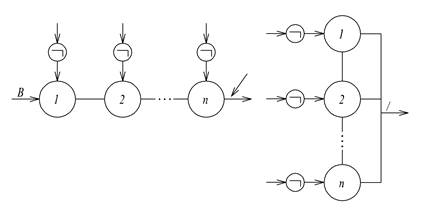
а) б)
Рис.1.2
Наряду с таблицами истинности применяются и другие способы задания функций алгебры логики, основанные на перечислении всех возможных наборов переменных.
Дата добавления: 2015-10-05; просмотров: 2515;
