Задание с помощью полного бинарного дерева

Для описания n-местной функции f (`х <sup>n</sup>) используется свойство бинарного дерева высоты n, заключающееся в том, что каждой висячей вершине в нем взаимно однозначно соответствует некоторый набор значений вектора`хⁿ. Соответственно, этой висячей вершине можно приписать такое же значение истинности, которое имеет на данном наборе функция f. В качестве примера (рис.1.3) приведем задание с помощью бинарного дерева рассмотренной выше трехместной функции f = (10110110).

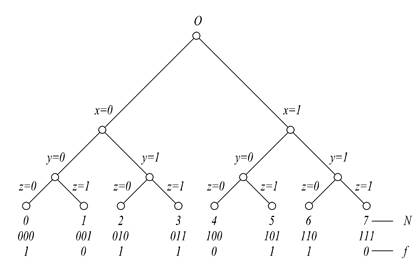
Рис.1.3

Первый ряд цифр, приписанных висячим вершинам дерева, обозначает лексикографический номер набора, второй ― сам набор, а третий ― значение функции на нем.

Задание с помощью n - мерного единичного куба В ⁿ

Поскольку вершины В ⁿ также можно взаимно однозначно отобразить на множество всех наборов`хⁿ, то n-местную функцию f(хⁿ) можно задать, приписывая ее значения истинности соответствующим вершинам куба В ⁿ. На рис.1.4 показано задание функции f =(10110110)на кубе В³. Значения истинности приписаны вершинам куба.

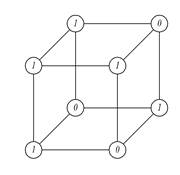
Рис.1.4

Определение. Алгеброй логики называют множество булевых констант и переменных вместе с введенными на них логическими связками.