Следствия.

1. Мощности бесконечных множеств так же, как и конечных, могут различаться.

2. Множеств с максимально возможной мощностью не существует, поскольку для любого множества М всегда можно рассмотреть множество его подмножеств [М]. В теории множеств доказана теорема Цермело, которая утверждает, что для произвольных множеств А и В всегда есть только три возможности:
а) ½А½<½В½; б) ½А½>½В½; в) ½А½ = ½В½.Отсюда следует, что несравнимых по мощности множеств не существует.

Определение. Множествами мощности континуум называют множества, эквивалентные множеству вещественных чисел на отрезке [0,1]. Обозначается данный вид мощности С либо À.

Можно показать путем построения соответствующего взаимно однозначного отображения, что между мощностями счетного множества и множества мощности континуум существует следующая связь: ½[N]½ = 2^N = C.

В отличие от счётных, множества мощности континуум нельзя упорядочить. Множество вещественных чисел на отрезке [0;1] является как бы эталоном для других множеств мощности континуум, с которым их сравнивают путём построения взаимно однозначных отображений. Г.Кантором дано прямое доказательство несчетности данного множества с помощью диагональной процедуры.

Теорема 2.5 (Г.Кантор). Множество вещественных чисел на отрезке [0;1] несчетно.

Доказательство. Любое из этих чисел можно задать в виде конечной либо бесконечной десятичной дроби α=0,α₁α₂α_3… , где 0≤ α_i ≤9. Представим каждую конечную дробь α=0,α₁α₂α_3… α_k в бесконечной форме: α=0, 0,α₁α₂α_3…(α_k-1)99…. Для числа 1 получаем: 1 = 0,99… .

Допустим, рассматриваемое множество счетно. При этом все вещественные числа на отрезке [0; 1] могут быть упорядочены в виде счетного списка, в который каждое из них входит ровно один раз и представлено бесконечной последовательностью десятичных знаков:

β₁=0, β₁₁ β₁₂ β₁₃ β_14…

β₂=0, β₂₁ β₂₂ β₂₃ β_24…

β₃=0, β₃₁ β₃₂ β₃₃ β_34…

β₄=0, β₄₁ β₄₂ β₄₃ β_44…

…

Построим бесконечную дробь γ=0,γ₁γ₂γ_3… по следующему правилу: еcли β_ii=1, то γ_i = 2, а еслиβ_ii≠1, то γ_i = 1. Из алгоритма построения следует, что дробь γ не совпадает ни с одним из чисел β_i, посколькуγ_i ≠ β_ii . Следовательно, вещественное число γ, принадлежащее отрезку [0; 1], не содержится в списке. Получаем противоречие с допущением о возможности упорядочения всех вещественных чисел из данного отрезка.

Пример 4. Найти мощность множества R вещественных чисел на всей числовой оси (–¥;+¥).

Решение. Очевидно,½R½ ³ С, поскольку отрезок [0;1] Ì R. Докажем строгое равенство ½R½= С путем построения взаимно однозначного отображения f множества А = [0;1]на R. С помощью одних линейных отображений невозможно взаимно однозначно отобразить конечный отрезок на бесконечную область. Данным свойством обладает тригонометрическая функция у = tg(х). Но она действует на отрезке [–p/2; +p/2],поэтому вначале необходимо взаимно однозначно отобразить отрезок [0;1] (множество А) на отрезок [–p/2; +p/2] (который обозначим множеством В), а затем множество В взаимно однозначно отобразить на R.

Первая задача может быть решена с помощью линейного отображения. Поскольку оно имеет два неизвестных коэффициента (С₀,С₁), то их можно найти, подставив в уравнение связи
b = С₀ a + С₁две пары значений из множеств А и В, которые должны взаимно однозначно отображаться друг в друга. Если взять в качестве таких пар минимальные и максимальные значения на отрезках (0 « –p/2; 1« + p/2), то множества точек, лежащие между ними, взаимно однозначно отобразятся друг на друга и задача будет выполнена. Подставляя выделенные пары в уравнение связи, получим систему двух уравнений:

– p/2= С₀ × 0+ С₁;

+p/2= С₀ × 1+ С₁.

Решая систему (например, методом исключения), получим:

С₀ = p ; С₁ = –p/2.

Взаимно однозначное отображение множества А на В (обозначим его g: А® В) примет вид: a Î A, g(а) = pа – p/2 = b Î B.

Для взаимно однозначного отображения множества В на R (обозначим его h: В ® R) используем функцию tg: b Î B, h(b) =
= tg(b) = r Î R.

Итоговое отображение f: A® R представим в виде композиции f = h g. Так как h и g взаимно однозначны, то и f по свойству композиций будет взаимно однозначным. Подставляя уравнение b(а)в зависимость r(b), найдем уравнение для отображения f, связывающее элементы аÎA с элементами rÎR: r = tg(pa – p/2).

Из факта построения взаимно однозначного отображения f:A® R по определению следует эквивалентность множеств A и R. Отсюда получим:½R½ = ½A½ = С.

С точки зрения мощности, множество всех точек, лежащих внутри и на границе квадрата[0;1] ´ [0;1], эквивалентно мощности всех точек на отрезке[0;1].

Теорема 2.6 (Г.Кантор).Множество всех точек декартова квадрата[0;1] ´ [0;1] имеет мощность континуум.

Доказательство. Построим взаимно однозначное отображение всех точек из квадрата [0;1] ´ [0;1] на множество вещественных точек отрезка[0;1].

Как и при доказательстве Теоремы 2.5, каждое из вещественных чисел, задающих координаты точек квадрата [0;1] ´ [0;1] или отрезка[0;1],представим в виде бесконечной десятичной дроби α = 0, α₁ α₂ α_3…, где 0 ≤ α_i ≤ 9. Все конечные дроби α = 0, α₁ α₂ α_{3 …} α_k для единообразия задаем в эквивалентной бесконечной форме: α = 0, α₁ α₂ α_{3 …}(α_k-1)99…. В том числе: 1 = 0,99… .

При выбранном способе представления каждой точке отрезка соответствует одна бесконечная десятичная дробь х = 0, х₁ х₂ х_3…, задающая ее координату на отрезке. Каждой точке квадрата — две дроби х = 0, х₁ х₂ х_{3 …} и у = 0, у₁ у₂ у_3…, которые равны ее декартовым координатам по осям.

Искомое взаимно однозначное отображение строим следующим образом. Каждой бесконечной десятичной дроби х = 0, х₁ х₂ х_{3 …}, задающей координату точки на отрезке [0;1], ставим в соответствие две дроби х´ = 0, х₁´ х₂´ х₃´ _… и у´= 0, у₁´ у₂´ у₃´_…, которые однозначно задают точку квадрата [0;1] ´ [0;1], по следующему правилу:

х₁´= х₁, у₁´= х₂, х₂´= х₃ , у₂´= х₄ ,…, х_n´= х_2n-1 , у_n´= х_2n.

Отображение является однозначным, имеет обратное отображение (х´,у´)®х, которое также однозначно. Следовательно, оно является взаимно однозначным и | [0;1] ´ [0;1]| = С, ч.т.д.

Аналогично можно доказать мощность континуум для всех точек куба [0;1] ³ = [0;1] ´ [0;1] ´ [0;1]и других более высоких декартовых степеней [0;1]ⁿ множества [0;1].

Полученный результат был удивителен для всех математиков, в том числе — для самого Г.Кантора, поскольку он входил в противоречие с понятием пространственной размерности объектов. Однако построенное отображение не является непрерывным в обе стороны, что является в математике достаточным условием для сохранения размерности.

Пример 5. Найти мощность множества R² точек на декартовой плоскости.

Решение. Используя отображение вида r = tg(pa -p/2) из Примера 4, можно взаимно однозначно отобразить все точки декартовой плоскости на декартов квадрат [0;1] ´ [0;1], мощность которого, как доказано в Теореме 2.6, равна континууму. Следовательно, | R²| = С.

Замечание. Так как процесс порождения множеств с большей мощностью бесконечен, то рассмотрев множество [А]всех подмножеств континуального множества А, получим множество2^А, мощности большей, чем континуум:½[А]½ = 2^C > С. Мощность 2^C имеет, в частности, множество всех функций, определённых на R .

Применение теоремы Кантора-Бернштейна значительно упрощает доказательство эквивалентности множеств мощности континуум одинаковой размерности. Для этого проще всего воспользоваться масштабным изменением размеров объектов, которое можно выполнить линейными преобразованиями с ненулевыми линейными коэффициентами, задающими взаимно однозначные отображения.

Пример 6. Найти мощность множества A точек, принадлежащих кругу радиуса r = 0,5 с центром в точке (1;1) на декартовой плоскости.

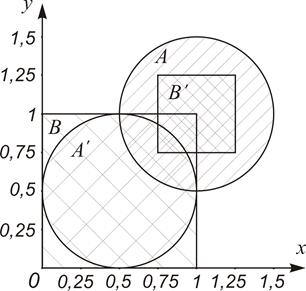
Рис.2.4

Решение. Докажем эквивалентность А множеству точек квадрата [0;1] ´ [0;1] (множество В, рис.2.4).

1. Вначале докажем эквивалентность А некоторому подмножеству В. Используя взаимно однозначное отображение х¢ = 1 · х - 0,5; у¢ = 1·у - 0,5, отобразим круг А на круг А¢, расположенный внутри В. Отсюда следует: |A¢| =|A| , A¢ Ì B.

2. Докажем, что В эквивалентно подмножеству А. При помощи взаимно однозначного отображения х¢ = 0,5·х + 0,75; у¢ = 0,5·у + 0,75, квадрат В отобразим на квадрат меньшего размера В¢, расположенный внутри круга A. Отсюда следует: |В¢| = |В| , В¢ Ì А.

По теореме Кантора-Бернштейна из 1 и 2 следует: |А| = |В| . Отсюда с учетом результатов Теоремы 2.6 получим: |A| = С.

ЗАДАЧИ

1. Найти мощность:

а) всех вещественных чисел в интервале [5;10];

б) множества вещественных чисел (–¥;– r] È (r; +¥), где r — некоторое положительное вещественное число;

в) множества вещественных чисел в объединении отрезков вида [2i;2i+1), где i Î Z;

г) множества вещественных чисел (–¥;0]È (1;+¥);

д) интервалов (r₁; r ₂), где r₁ и r ₂ - рациональные числа;

е) множества всех точек на окружности радиуса 1 с центром в точке (0; 0);

ж) множества точек на параболе у = (х–2)² при –¥ < х < +¥ .

2. Построить пример взаимно однозначного отображения:

а) множества N₁₀целых чисел, кратных 10, на множество N₂четных чисел;

б) множества вещественных чисел [0;4] на множество вещественных чисел [0;4] È (7;10];

в) множества всех окружностей на плоскости на множество всех квадратов на плоскости со сторонами, параллельными осям координат.

3. Построить взаимно однозначное отображение отрезка [0;1] на положительную полуось [0;+¥).

4. Существует ли взаимно однозначное отображение:

а) множества всех вещественных чисел R на множество всех целых чисел Z?

б) множества всех рациональных вещественных чисел на множество всех целых чисел?

5. Привести примеры счетных подмножеств на множествах:

а) всех прямых на плоскости;

б) шаров в пространстве;

в) векторов в n-мерном пространстве.

6. Будут ли иметь одинаковую мощность:

а) множества N₃ и N₄ всех натуральных чисел, кратных соответственно 3 и 4?

б) множества N³₃ и N³₄ всех трехзначных в десятичной системе счисления натуральных чисел, кратных 3 и 4?

7. Доказать с применением теоремы Кантора-Бернштейна эквивалентность множеств точек:

а) шара c радиусом R>0 и соответствующей ему сферы,

б) 3-мерного пространства и прямой линии в нем.

Глава 3. БИНАРНЫЕ ОТНОШЕНИЯ НА МНОЖЕСТВАХ