Алгебра висловлювань.
1) Висловлювання. Операції над висловлюваннями.
2) Конструювання складних висловлювань.
3) Класифікації формул алгебри висловлювань.
Під висловлюванням розуміється таке речення, яке або істинне або хибне. Висловлювання не може бути одночасно і хибним, і істинним. Позначимо істинне висловлювання символом 1, а висловлювання , що є хибним символом 0. Введемо функцію λ , яка задається на сукупності всіх висловлювань і приймає значення в двоелементеій множині {0,1} за наступним правилом:
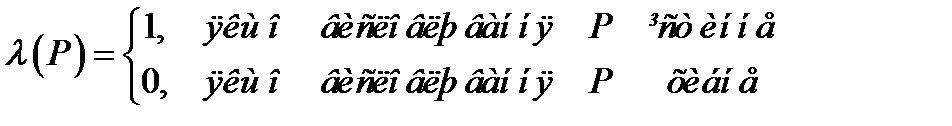
Функція λ називається функцією істинності, а значення λ(P) логічним значенням або значенням істинності висловлювання P. Будемо позначати висловлювання великими літерами латинського алфавіту або ж літерами з індексами.
Приклади : 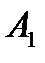 :”Київ столиця України”;
:”Київ столиця України”;
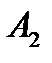 :”Чернігів розташований на березі Десни”;
:”Чернігів розташований на березі Десни”;
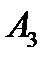 :”7
:”7 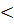 4” ;
4” ;
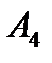 :”Шевченко – великий укр.математик”.
:”Шевченко – великий укр.математик”.
λ ( 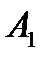 )=1 ; λ(
)=1 ; λ( 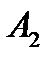 ) = 1; λ(
) = 1; λ( 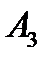 )= 0; λ(
)= 0; λ( 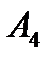 )=0
)=0
Запереченням висловлювання P називається нове висловлювання P (не P), яке є істинним, коли висловлювання.P є неправдою і є неправдою якщо висловлювання P є істинним, іншими словами логічне значення 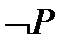 зв'язане з логічним значенням вхідного висловлювання P як показано в наступній таблиці, яку називають таблицею істинності операції заперечення.
зв'язане з логічним значенням вхідного висловлювання P як показано в наступній таблиці, яку називають таблицею істинності операції заперечення.
| Λ(P) | Λ( P) |
Застосуємо операцію заперечення до висловлювання 
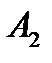 : “Чернігів розташований на березі Десни”
: “Чернігів розташований на березі Десни”
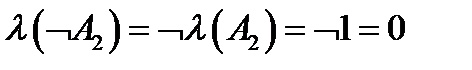 .
.
Тобто висловлювання 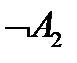 є неправдою.
є неправдою.
Кон'юнкцією двох висловлювань P і Q називають нове висловлювання, яке позначається P 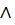 Q , яке є істинним тоді і тільки тоді, коли обидва вхідні висловлювання є істинними. І неправдою у всіх інших випадках. Логічне значення P
Q , яке є істинним тоді і тільки тоді, коли обидва вхідні висловлювання є істинними. І неправдою у всіх інших випадках. Логічне значення P  Q зв'язане з логічним значенням висловлювань P і Q, таблицею істинності операції кон'юнкції .
Q зв'язане з логічним значенням висловлювань P і Q, таблицею істинності операції кон'юнкції .
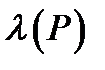
| 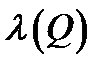
| 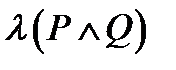
|
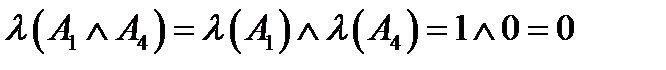
Диз'юнкцією двох висловлювань – P і Q називається нове висловлювання, що позначають P  Q (P або
Q (P або  Q), яке є істинним в тих випадках, коли хоча б одне з вхідних висловлювань є істинним і є неправдою коли обидва висловлювання є неправдою. P
Q), яке є істинним в тих випадках, коли хоча б одне з вхідних висловлювань є істинним і є неправдою коли обидва висловлювання є неправдою. P  Q – це таке висловлювання, логічне значення якого зв'язане з логічним значенням вхідних висловлювань P і Q таблицею істинності операції диз'юнкція
Q – це таке висловлювання, логічне значення якого зв'язане з логічним значенням вхідних висловлювань P і Q таблицею істинності операції диз'юнкція
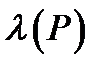
| 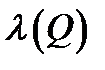
| 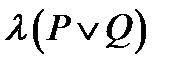
|
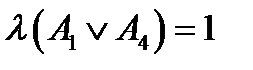 .
.
Імплікацією двох висловлювань 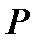 і
і 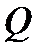 називають нове висловлювання, яке позначається P→Q (якщо P то Q) або (з P випливає Q), і є неправдою коли висловлювання P є істинним , а висловлювання Q є неправдою, у всіх інших випадках приймає значення істина. Логічне значення висловлювання P→Q зв'язане з логічним значеннями вхідних висловлювань P і Q таблицею істинності операції імплікація.
називають нове висловлювання, яке позначається P→Q (якщо P то Q) або (з P випливає Q), і є неправдою коли висловлювання P є істинним , а висловлювання Q є неправдою, у всіх інших випадках приймає значення істина. Логічне значення висловлювання P→Q зв'язане з логічним значеннями вхідних висловлювань P і Q таблицею істинності операції імплікація.
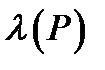
| 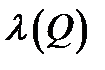
| 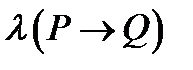
|
Еквівалентністю двох висловлювань P і Q називається нове висловлювання, яке позначається P↔Q (P еквівалентно Q) , яке істинне тоді і тільки тоді, коли P і Q є або істинними або хибними одночасно. Логічне значення P↔Q зв'язане з логічним значеннями вхідних висловлювань P і Q таблицею істинності операції еквівалентність.
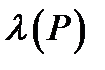
| 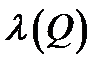
| 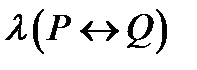
|
Зауваження:
В алгебрі висловлювань нас цікавлять тільки логічні значення висловлювань або значення істинності, а не їх зміст. Тому кожне з введених означень (заперечення, кон'юнкція диз'юнкція, імплікація ) можна розглядати як визначення деякої дії над символами 0 і 1. Тобто як визначення деякої операції на дво-елементній множині. Враховуючи правило дії з символами 0 і 1, що визначені таблицями істинності операцій (заперечення, кон'юнкції диз'юнкції, імплікації, еквівалентності) можна записати:
λ(P)=(λ(P));
λ(P 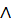 Q)=λ(P)
Q)=λ(P) 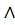 λ(Q);
λ(Q);
λ(P 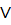 Q)=λ(P)
Q)=λ(P) 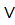 λ(Q);
λ(Q);
λ(P→Q)=λ(P)→λ(Q);
λ(P↔Q) = λ(P)↔λ(Q).
Конструювання складних висловлювань.
Розглянемо висловлювання.
Якщо Т.Г.Шевченко – великий український математик і Київ – столиця України, то 7 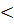 4.
4.
Зауважимо, що нас не цікавить зміст висловлювання, а тільки його логічне значення. В дане висловлювання входять висловлювання 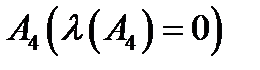 ,
, 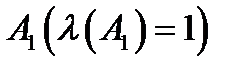 ,
, 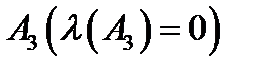 .
.
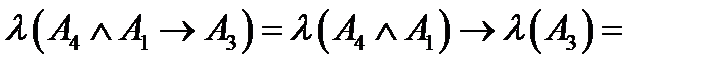
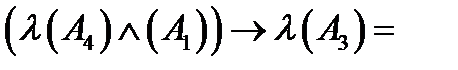
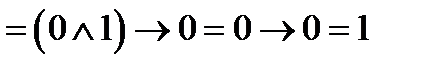 .
.
Дане висловлювання є істинним. Воно конструюється з простих висловлювань 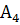 ,
, 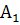 ,
, 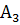 . Для визначення істинності складного висловлювання необхідно до перших двох застосувати кон'юнкцію, а потім до отриманого висловлювання і висловлювання
. Для визначення істинності складного висловлювання необхідно до перших двох застосувати кон'юнкцію, а потім до отриманого висловлювання і висловлювання 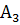 застосувати операцію імплікації. Цей словесний опис схеми конструювання складного висловлювання можна замінити описом символічним:
застосувати операцію імплікації. Цей словесний опис схеми конструювання складного висловлювання можна замінити описом символічним:
( 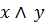 )
) 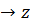 , де
, де 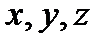 - деякі символи (змінні) замість яких можна підставити будь-які конкретні висловлювання.
- деякі символи (змінні) замість яких можна підставити будь-які конкретні висловлювання.
Ця схема може бути застосована до будь-яких висловлювань, а не тільки до висловлювань 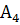 ,
, 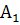 ,
, 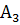 . В цю формулу замість x, y, z можна підставляти конкретні висловлювання після чого вся формула буде перетворюватися в зіставне, складне висловлювання. Змінні замість яких можна підставити висловлювання називаються пропозиціональними змінними або змінними висловлювання. Будемо позначати пропозиціональні змінні висловлювання великими буквами P, Q, X, Y, Z.
. В цю формулу замість x, y, z можна підставляти конкретні висловлювання після чого вся формула буде перетворюватися в зіставне, складне висловлювання. Змінні замість яких можна підставити висловлювання називаються пропозиціональними змінними або змінними висловлювання. Будемо позначати пропозиціональні змінні висловлювання великими буквами P, Q, X, Y, Z.
Дамо таке визначення:
1) Кожна окрема пропозиціональна змінна є формулою алгебри висловлювань.
2) Якщо 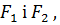 є формулами алгебри висловлювань, то формули
є формулами алгебри висловлювань, то формули 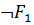 ,
, 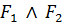 ,
, 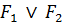 ,
, 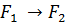 ,
, 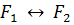 є формулами алгебри висловлювань.
є формулами алгебри висловлювань.
3) Ніяких інших формул крім тих, які отримані згідно пункту 1 і 2 не існує. Якщо у формулі алгебри висловлювань F( 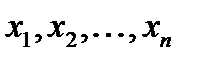 ) замість пропозиціональних змінних
) замість пропозиціональних змінних 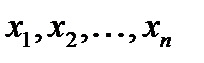 підставити конкретні висловлювання
підставити конкретні висловлювання 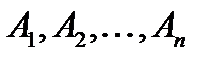 , то отримаємо деяке нове зіставне висловлювання F(
, то отримаємо деяке нове зіставне висловлювання F( 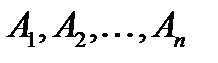 ). Дане висловлювання називається конкретизацією формул F(
). Дане висловлювання називається конкретизацією формул F( 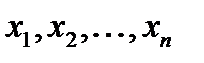 ) на виборі висловлювань
) на виборі висловлювань 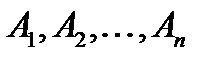 .
.
Теорема 1:
Логічне значення зіставного висловлювання F( 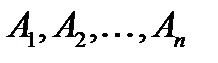 ) дорівнює значенню формули F
) дорівнює значенню формули F 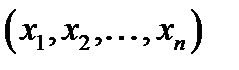 на наборі даних
на наборі даних 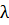 (
( 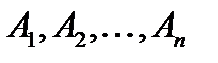 ).
).
Висновок:
Логічне значення зіставного висловлювання є значенням деякого виразу при відповідному наборі всіх пропозиціональних змінних, що входять у дане висловлювання. При цьому пропозиціональні змінні можуть приймати значення 0 чи 1. Сам вираз обчислюється шляхом застосування до значень 0 і 1 логічних дій, які регламентовані даним виразом. Логічні дії над 0 і 1 виконуються за правилами, які визначені таблицею істинності цих дій.
На основі теореми 1 можна для конкретної формули алгебри висловлювань знайти логічне значення всіх тих висловлювань, в які формула перетворюється при підстановці замість всіх її пропозиціональних змінних різних конкретних висловлювань. При цьому говорять про логічне значення самої формули і про логічне значення її пропозиціональних змінних.
Приклад 1:
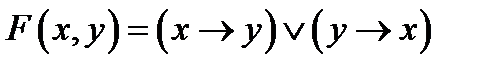
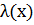
| 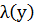
| 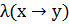
| 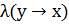
| 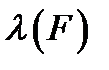
|
Зауваження. Перші два стовпчики і останній стовпчик таблиці задають відповідності між логічним значенням вхідного висловлювання і логічним значення зіставного висловлювання, яке отримане заданою формулою. Ці три стовпчики для формули 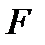 , інші два стовпчики є допоміжними.
, інші два стовпчики є допоміжними.
Приклад 2:
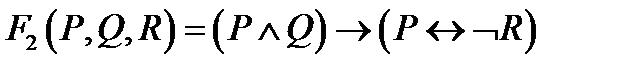
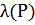
| 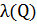
| 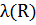
| 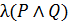
| 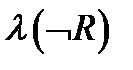
| 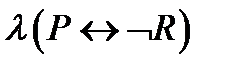
| 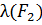
|
Класифікація формул алгебри висловлювань.
Формули алгебри висловлювань розподіляють на наступні типи:
а) ті, що виконуються;
б) тавтології;
в) ті, що спростовуються;
г) ті, що є тотожно неправдивими.
Формулу алгебри висловлювань 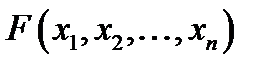 називають такою, яку можна виконати, якщо деяка її конкретизація є істинним висловлюванням, тобто існують такі конкретні висловлювання
називають такою, яку можна виконати, якщо деяка її конкретизація є істинним висловлюванням, тобто існують такі конкретні висловлювання 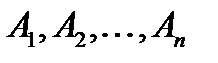 , які при підстановці в дану формулу замість змінних
, які при підстановці в дану формулу замість змінних 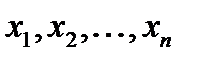 відповідно перетворюють її в істинне висловлювання. Таким чином, формула
відповідно перетворюють її в істинне висловлювання. Таким чином, формула 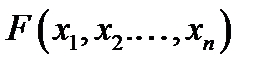 є такою, яку можна виконати , якщо існують такі конкретні висловлювання
є такою, яку можна виконати , якщо існують такі конкретні висловлювання 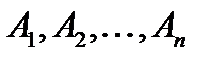 , що
, що 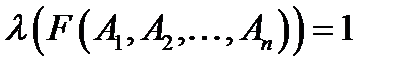 .
.
Формулу 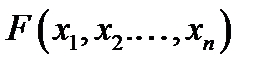 називають тавтологією, або тотожно істинною, якщо вона перетворюється в істинне висловлювання при будь-якій підстановці замість змінних конкретних висловлювань
називають тавтологією, або тотожно істинною, якщо вона перетворюється в істинне висловлювання при будь-якій підстановці замість змінних конкретних висловлювань 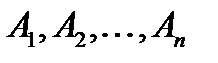 , тобто, якщо
, тобто, якщо 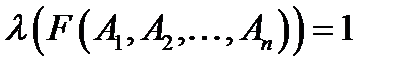 для будь-яких висловлювань
для будь-яких висловлювань 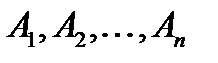 .
.
Для позначення тавтологій використовують знак , який ставиться перед формулою, що є тавтологією. Таким чином, запис 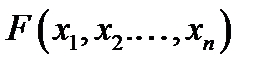 означає, що формула
означає, що формула 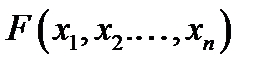 є тавтологією.
є тавтологією.
Можемо записати 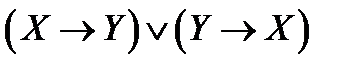 .
.
Формулу 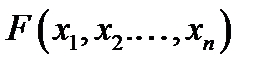 називають такою, що спростовується, якщо існують такі конкретні висловлювання
називають такою, що спростовується, якщо існують такі конкретні висловлювання 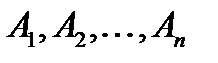 , які перетворюють дану формулу у висловлювання, яке є неправдою, тобто
, які перетворюють дану формулу у висловлювання, яке є неправдою, тобто 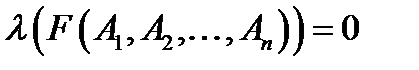 .
.
Формулу 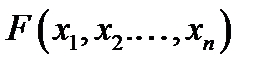 називають тотожно неправдивою (або протиріччям), якщо
називають тотожно неправдивою (або протиріччям), якщо 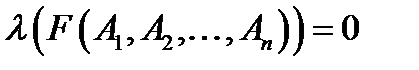 для будь-яких конкретних висловлювань
для будь-яких конкретних висловлювань 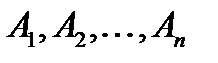 . Іншими словами, протиріччями є формули, які неможливо виконати.
. Іншими словами, протиріччями є формули, які неможливо виконати.
Ми з вами підійшли до фундаментального процесу дослідження математичними методами такої сфери, як область людського мислення. Побудована своєрідна система знаків (символічна мова логіки висловлювань) за допомогою якої можна спробувати виразити людську думку і прослідкувати отримання результату процесу мислення.
Ця мова базується на алфавіті, що складається :
а) пропозиціональних букв: 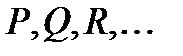 ;
;
б) символів логічних операцій: 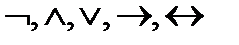 ;
;
в) технічних знаків: (,).
Словами побудованої мови є формули логіки висловлювань. Речення природної мови можуть бути переведені на символічну мову логіки висловлювань, де вони представленні формулами логіки висловлювань.
Формула представляє собою формальну послідовність знаків, що побудована за строгими правилами, порушення яких є недопустимим. Такий переклад висловлювань природної мови на символічну мову називають його формалізацією. Формула логіки висловлювань сама по собі не має ніякого змісту. Вона не є істинною і не є хибною. Дана формула перетворюється у висловлювання істинне, або таке, що є неправдою при любій підстановці замість всіх її пропозиціональних змінних конкретних висловлювань. Такий процес підстановки називають інтерпретацією даної формулт алгебри висловлювань.
Таким чином, існує два взаємно обернених процеси: формалізація та інтерпретація. Якщо є формула F і висловлювання А є результат її інтерпретації, то сама формула Fє формалізацією висловлювання А. з іншого боку, якщо існує висловлювання А і формула F є її формалізацією, то висловлювання А буде однією з інтерпретацій формули F.
Висновок.
Формалізація - це перехід від висловлювань природної мови до формули логіки висловлювань, а інтерпретація - перехід від формули логіки висловлювань до висловлювань природною мовою. Таблиця істинності, або таблиця значень логіки висловлювань – це таблиця, яка визначає логічне значення формули при будь-якій її інтерпретації.
Дата добавления: 2015-10-13; просмотров: 3209;
