Алгорифми Маркова

1) Підстановки Маркова.

2) Поняття нормального алгорифму Маркова.

3) Нормально-обчислювальні функції. Принцип нормалізації Маркова.

4) Еквівалентність теорій Тюрінга, Маркова та теорії частково-рекурсивних функцій.

Алгорифми Маркова представляють собою деякі правила по перебудові слів у відповідному алфавіті і результат роботи алгорифмів Маркова є слова деякого алфавіту.

1) Підстановки Маркова

Алфавітом є будь-яка непуста множина, її елементи є буквами алфавіту, а будь-які послідовності букв – словами алфавіту.

Слова, що не містять букв – пусті. 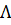- пусте слово.

Якщо A і B – два алфавіти, при чому 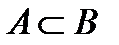(A підмножина В), то алфавіт В називають розширенням алфавіту А. Слова в алфавіті позначають латинськими буквами P, Q, R, або цими ж буквами з індексами .

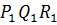Одне слово може бути складовою частиною іншого слова, тоді перше слово – підслово другого, або є входженням в друге слово.

Наприклад:

Наступні слова 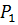- параграф, 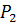- граф, 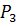- ра.

Слово 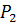є підсловом слова 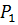, а слово 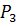є підсловом 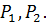При чому 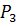входить у слово 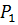двічі. Особливу увагу приділяють першому входженню.

Визначення:

Підстановка Маркова – операція над словами, що задаються за допомогою впорядкованої пари слів (P,Q) зміст якої полягає в наступному: в заданому слові R знаходять перше входження слова Р, якщо воно є. Не змінюючи частин слова R, замінюють в ньому це входження словом Q. Отримане слово є результатом застосування підстановки Маркова (P,Q) до слова R. Якщо входження P в слово R не існує, то вважається, що підстановку (P,Q) до слова R застосовувати не можна. Частковими випадками підстановок Маркова є підстановки з пустими словами.

Наприклад:

(

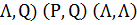
Функція 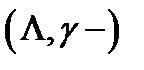буде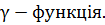

Функція ( 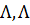) – функція.

Функція ( 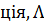) – функ.

Функція ( 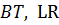) – застосовувати не можна.

Для позначень підстановок (P,Q) використовують запис (P 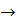Q) . Даний запис будемо називати формулою підстановки .

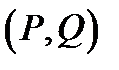Деякі підстановки є кінцевими або заключними, для позначення таких підстановок використовують запис (P 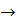.Q) далі цю підстановку називають формулою кінцевої підстановки.

Слово Pназивають лівою частиною, а слово Q називають правою частиною в формулі підстановки.

2) Нормальні алгорифми. Застосування нормальних алгорифмів до слів.

Впорядкований скінченний список підстановок

,

,

………

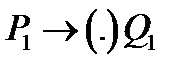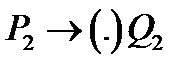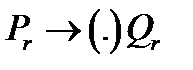
в алфавіті А називають схемою або записом нормального алгоритму в А. Запис крапки в дужках означає, що крапка може стояти в цьому місці, а може бути відсутньою. Дана схема визначає (детермінує) алгорифм перетворення слів, що називають нормальним алгорифмом Маркова.

Дамо точне визначення:

Нормальним алгорифмом Маркова в алфавіті А – називають наступне правило побудови послідовності слів 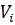в алфавіті А, виходячи з заданого слова 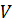в цьому ж алфавіті. В якості початкового слова 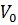в послідовності береться слово 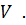Нехай для деякого і 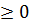слово 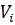побудоване і процес побудови послідовності, що розглядається ще не закінчився. Якщо при цьому в схемі нормального алгорифму не має формул, ліві частини яких входили б у 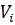, то 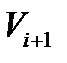вважають рівним 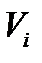і процес побудови послідовності вважається завершеним. Якщо в схемі є формули з лівими частинами, які входять до 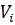, то в якості 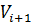береться результат Марковської підстановки правої частини першої з таких формул замість першого входження лівої частини в .

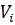Процес побудови послідовності ввпжається завершеним, якщо на даному кроці була застосована формула заключної підстановки і таким, що продовжується у протилежному випадку. Якщо процес побудови послідовності 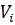, 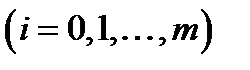обривається, то говорять, що нормальний алгорифм, який розглядається, можна застосувати до слова . Останній член W –послідовності називають результатом застосування нормального алгорифму до слова 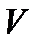. Кажуть, що нормальним алгорифм переробляє 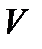в W.

Останній член 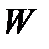послідовності називають результатом засьосування нормального алгоритму до слова . Говорять, що нормальний алгорифм переробляє 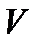у 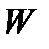. Послідовність 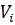будемо записувати наступним чином:

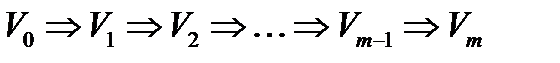, де

, .

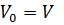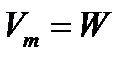Якщо алгорифм заданий в розширенні алфавіту А, то говорять, що він є нормальним алгорифмом на А.

Приклад 1. Нехай 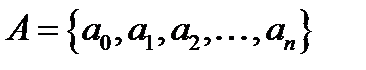- алфавіт. Розглянемо схему:

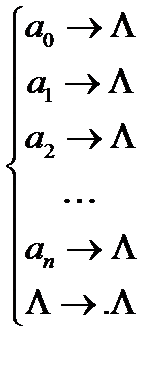
Дана схема визначає нормальний алгоритм, що перероблює будь-яке слово в алфавіті А в пусте слово.

.

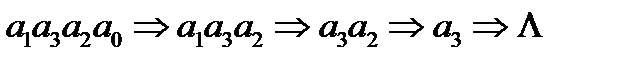Нормально обчислювальні функції . Принцип нормалізації Маркова.

Як і машини Т’юринга, нормальні алгорифми власне не проводять обчислень. Нормальні алгорифми перебудовують слова, замінюючи одні букви іншими по приписаним їм правилам. В свою чергу ми регламентуємо їм такі правила, результати застосування яких можна інтерпретувати як обчислення.

Приклад 2. В алфавіті 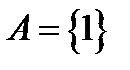задано схему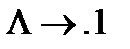

Даний нормальний алгорифм реалізує (обчислює) функцію .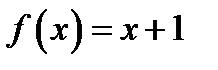

(слова ).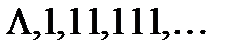

Приклад 3. Задано функцію ,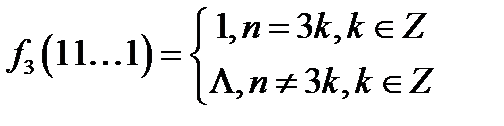

де 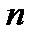- число одиниць в слові .

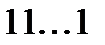Розглянемо нормальний алгорифм в алфавіті .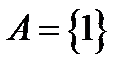

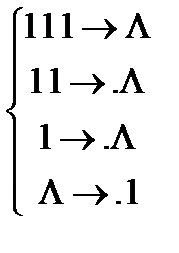
Розглянутий нормальний алгорифм обчислює (реалізує) функцію .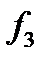

;

.

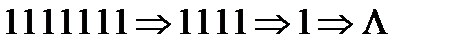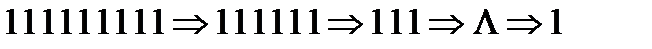Визначення.

Функція 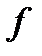, яка задана на деякій множині слів алфавіта А, називають нормально обчислювальною функцією, якщо знайдеться таке розширення В даного алфавіта 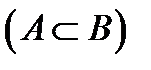і такий нормальний алгорифм в В, що кожне слово 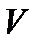в алфавіті А з області визначення функції 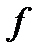цей алгорифм перероблює в слово .

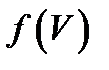Нормальні алгорифми прикладів 2 і 3 показують, що функції 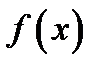та 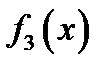е нормально обчислювальними. Зауважимо, що нормальні алгорифми ми побудували в тому самому алфавіті А, тобто алфавіт а не потрібно було розширяти .

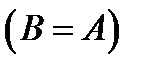Побудуємо нормальний алгорифм для обчислення функції 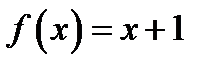не в одиничній системі, а в десятковій. В якості алфавіта А візьмемо перелік арабських цифр 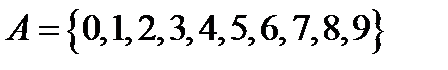, а нормальний алгорифм побудуємо в його розширенні .

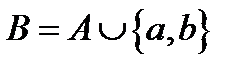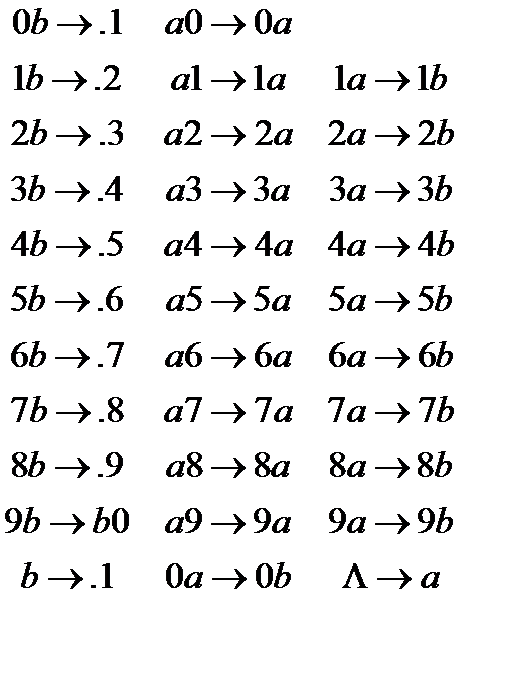
В даному прикладі нормальний алгорифм, побудований в алфавіті В, що є розширенням алфавіту А. Але цей алгорифм слова а алфавіті А переробляє знову в слова в алфавіті А. В такому випадку говорять, що алгорифм заданий над алфавітом А .

А.А.Марков, що створив теорію нормальних алгорифмів висунув гіпотезу, яка отримала назву “Принцип нормалізації Маркова”. Згідно з цим принципом для знаходження значення функції, яка задана на деякому алфавіті тоді і тільки тоді існує алгоритм, коли ця функція є нормально-обчислювальною. Так як і теза Черча, теза Т’юрінга, принцип нормалізації Маркова не може бути доведений з математичної точки зору. Даний принцип був сформульований на підґрунті математичного та практичного досвіду.

Еквівалентність теорій:

Теорема 1:

Функція, що є обчислювальною за Т’юрінгом є також нормально обчислювальною.

Теорема 2:

Функція, що є нормально обчислювальною є обчислювальною за Т’юрінгом.

Такі самі теореми існують по відношенню до частково-рекурсивних функцій.

Теорема 3: Наступні класи функцій, що задані на натуральних числах і приймають натуральні значення співпадають:

а) клас всіх функцій, що є обчислювальними за Т’юрінгом;

б) клас всіх частково-рекурсивних функцій;

в) клас всіх нормально обчислювальних функцій.

Ця теорема є опосередкованим підтвердженням тез Черча, Маркова, Т’юрінга. Дійсно. Якщо один в вище зазначений класів був би ширший за інших, то дві тези були б спростовані, що досі не підтверджено практикою.