Доказательство теоремы Маркова.
Теорема (Маркова). Если 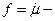 функция Марковского типа, то её непрерывная дробь сходится к
функция Марковского типа, то её непрерывная дробь сходится к 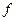 равномерно внутри области
равномерно внутри области 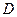 .
.
Доказательство. Рассмотрим последовательность функций 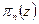 . Они все голоморфные в области D, где
. Они все голоморфные в области D, где 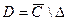 - плоскость с разрезом. В частности, в бесконечности функции тоже голоморфны.
- плоскость с разрезом. В частности, в бесконечности функции тоже голоморфны.
Докажем, что внутри область D. 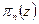 равномерно ограниченная последовательность. Зафиксируем компакт
равномерно ограниченная последовательность. Зафиксируем компакт 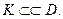 Обозначим:
Обозначим: 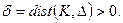
Оценим: если 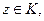 то
то 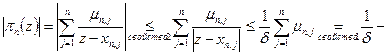 таким образом, получили равномерную оценку.
таким образом, получили равномерную оценку. 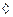
Тогда применим теорему Монтеля 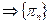 - предкомпактная. Следовательно она имеет предельные точки. Обозначим:
- предкомпактная. Следовательно она имеет предельные точки. Обозначим: 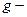 предельные точки
предельные точки 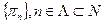 . Тогда
. Тогда 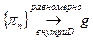 по некоторой подпоследовательности,
по некоторой подпоследовательности, 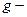 голоморфна в области D по 1 теореме Вейеерштрасса. Тогда
голоморфна в области D по 1 теореме Вейеерштрасса. Тогда 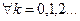
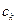 - Лорановсий коэффициент для функции
- Лорановсий коэффициент для функции 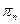 .
. 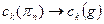 для некоторой подпоследовательности
для некоторой подпоследовательности 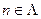 . Но, по построению,
. Но, по построению, 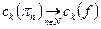 , значит ряды совпадают:
, значит ряды совпадают: 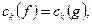 т.е.
т.е. 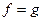 в окрестности
в окрестности 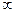 (там, где ряды сходятся). Но
(там, где ряды сходятся). Но 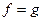 всюду в области D, тогда по теореме единственности, мы доказали, что
всюду в области D, тогда по теореме единственности, мы доказали, что 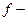 единственная предельная точка последовательности
единственная предельная точка последовательности 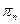 , а тогда
, а тогда 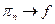 (из матана).
(из матана). 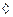
|
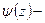 функцию обратную к функции Жуковского, а именно:
функцию обратную к функции Жуковского, а именно: 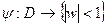 т.е. область с разрезом в единичный круг. Причём
т.е. область с разрезом в единичный круг. Причём 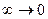 ,
, 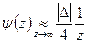 ,
, 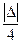 называется логарифмической ёмкостью. В частности, когда
называется логарифмической ёмкостью. В частности, когда 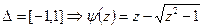 . Если отрезок другой, то надо сделать замену переменной. Обозначим
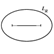
. Если отрезок другой, то надо сделать замену переменной. Обозначим 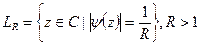 - линия уровня этой функции.
- линия уровня этой функции. 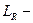 эллипс с фокусами в концах отрезка.
эллипс с фокусами в концах отрезка.
Утверждение. 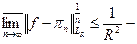 оценка скорости сходимости.
оценка скорости сходимости.
Доказательство. Рассмотрим функцию 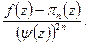 Она голоморфна в области D. Знаменатель в 0 нигде не обращается, кроме
Она голоморфна в области D. Знаменатель в 0 нигде не обращается, кроме 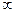 . В ней в числителе 0 порядка
. В ней в числителе 0 порядка 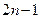 , в знаменателе – ноль порядка
, в знаменателе – ноль порядка 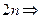 ноль 1ого порядка
ноль 1ого порядка 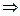 устранимая особая точка.
устранимая особая точка.
|
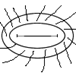
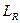 и проведём ещё один с
и проведём ещё один с 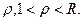 Воспользуемся принципом максимума модуля:
Воспользуемся принципом максимума модуля:
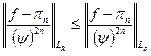 эквивалентно:
эквивалентно: 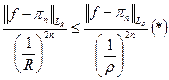
Применим этот принцип к заштрихованной области (мах модуля достигается на границе).
При доказательстве теоремы Маркова, мы доказали: 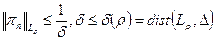 , но
, но 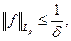 т.к. если
т.к. если 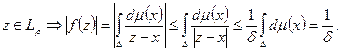 Тогда
Тогда 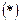 имеет вид:
имеет вид: 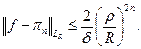 Теперь извлечём
Теперь извлечём 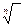 из обеих частей неравенства и к
из обеих частей неравенства и к 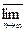 .
. 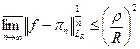 , т.е.
, т.е. 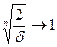 как предел от const. Т.к.
как предел от const. Т.к. 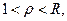 то
то 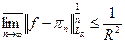 .
. 
Дата добавления: 2015-09-02; просмотров: 973;