Доказательство. Докажем теорему индукцией по глубине формулы U.
Докажем теорему индукцией по глубине формулы U.
1. Базис индукции.Покажем, что если f =  , то
, то 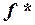 представляется формулой
представляется формулой  . Запишем цепочку равенств:
. Запишем цепочку равенств:
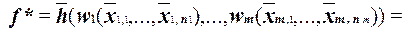
= 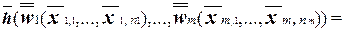
= 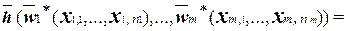
=  .
.
2. Индуктивное предположение. Предположим, что доказываемое в свойство выполняется для всех формул, глубина которых не превосходит n.
3.Индуктивный переход. Пусть f = U(g1,..., gn), где U(g1,..., gn) - это формула глубины n + 1, составленная с помощью символов переменных и функций g1,..., gn
Предположим, что U = h(U1, . . . , Un), где для формул U1, . . . , Un и представляемых ими булевских функций w1, . . . , wn справедлива доказываемая теорема.
Тогда аналогично доказательству базиса индукции можно показать, что 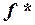 =
= 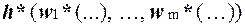 .
.
Поскольку всякая функция  представляется формулой
представляется формулой 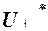 , то
, то 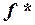 представляется формулой
представляется формулой 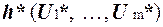 , т.е. формулой U(
, т.е. формулой U(  ,...,
,..., 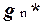 ).
).
Дата добавления: 2015-09-18; просмотров: 774;
