ОПРЕДЕЛЕНИЕ. Функция f называется самодвойственной, если f = f*.

Функция f называется самодвойственной, если f = f*.

То есть всякая самодвойственная функция на любых двух противоположных наборах значений переменных принимает противоположные значения. Примерами самодвойственных функций являются тождественная функция f(x) = x и отрицание f(x) = .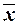

Множество всех самодвойственных функций обозначается как S.

Установленное ранее свойство симметричности расположения противоположных наборов в табличном задании булевских функций позволяет использовать следующую схему построения табличного задания функции, двойственной к заданной функции.

Пусть f(x₁, . . . , x_n) - произвольная булевская функция, заданная таблично.

1. Выпишем столбец значений f в обратном порядке.

2. В полученном столбце выполним замену всякого значения в нем на противоположное значение.

Полученный в результате столбец значений функции представляет собой столбец значений двойственной функции f*. Действительно, первое преобразование позволяет по столбцу значений функции f(x₁, . . . , x_n)получить столбец значений функции f( ).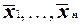

Второе преобразование переводит функцию f( 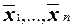) в ее отрицание, 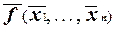т.е. окончательная функция - это f*.

Если функция f задана формулой, то для получения формульного представления функции f* можно воспользоваться следующей теоремой.

ТЕОРЕМА 4.7 (О формуле для двойственной функции)

Пусть f(x₁, . . . , x_n)представляется формулой U (g₁,..., g_n). Тогда функция f* представляется формулой

U* = U(g*₁, . . . , g*_n).