ФУНКЦИИ, СОХРАНЯЮЩИЕ НОЛЬ

СПЕЦИАЛЬНЫЕ КЛАССЫ БУЛЕВСКИХ

ФУНКЦИЙ

ОПРЕДЕЛЕНИЕ

Множество функций B 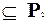называется замкнутым классом, если [B] = B.

Например, множество {x, 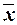} является замкнутым классом. Рассмотрим пять специальных классов булевских функций, свойства которых будут использованы при нахождении простых необходимых и достаточных условий полноты произвольных систем функций в P₂.

ФУНКЦИИ, СОХРАНЯЮЩИЕ НОЛЬ

Обозначим как Т₀ множество всех таких булевских функций, которые на нулевом наборе значений переменных принимают значение 0.

О таких функциях говорят, что они сохраняют 0, т.е. множество б.ф., сохраняющих ноль, это:

Т₀ = {f(x₁,...,x _n) ½ f(0,...,0) = 0}.

Сформулируем простейшие свойства класса T₀.

1. Класс T₀ является замкнутым классом функций.

Для проверки справедливости последнего утверждения достаточно проверить, что всякая формула U(f₁, . . . , f_p), составленная с помощью функций f₁, . . . , f_p, сохраняющих ноль, представляет функцию f_U, которая также сохраняет ноль.

Проведем обоснование этого свойства в соответствии с определением понятия формулы над классом функций.

1.1.Если U = f(x₁,. . . , x_n), где f(x₁, . . . , x_n)ÎT₀, то
f (0, . . . , 0) = 0и f_U = f.

1.2.Если U = f (U₁,...,U_n), где f (x₁, . . . , x _n) Î T₀, а
U₁, . . . ,U_n - это или символы переменных или подформулы формулы U, составленные с помощью функций из T₀ и символов переменных. Заметим, что поскольку обозначение переменной представляет тождественную функцию I(x) = x, то U₁, . . . ,U_n можно рассматривать как подформулы, представляющие некоторые функции 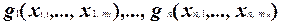из класса T₀. Тогда функция f( 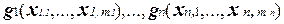) также принадлежит классу T₀.

Действительно, f(g₁(0,. . . , 0),. . . , g_n (0, . . . ,0))= f(0, . . . ,0)=0.

2. Определим число различных функций переменных
x₁, . . . , x_n, которые содержатся в T₀.

Поскольку функции из T₀ на всех наборах значений переменных, отличных от нулевого набора, принимают произвольные значения, и таких ненулевых наборов 2ⁿ-1, то в T₀ содержится ровно 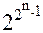различных булевских функций n переменных.