Доказательство окончено. Определим число самодвойственных функций, имеющих n переменных

Пример.Пусть U = 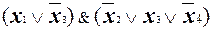. Тогда
U* = .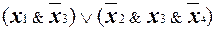

Определим число самодвойственных функций, имеющих n переменных. Из условия самодвойственности следует, что на противоположных наборах значений переменных всякая 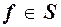принимает противоположные значения. Поэтому всякая 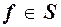однозначно определяется своим заданием на наборах верхней половины табличного задания булевских функций n переменных, то есть на 2^n-1 наборах.

Следовательно, число функций n переменных вS равно .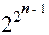

Покажем, что множество функций S является замкнутым классом. Поскольку тождественная функция f(x) = x является самодвойственной, то для доказательства замкнутости класса всех самодвойственных функций достаточно проверить, что если
h = 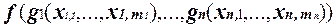, где f, g₁, . . . , g_n - это самодвойственные функции, то h = h*.

Воспользуемся теоремой о формуле для двойственной функции. Тогда h* = 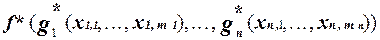= = = 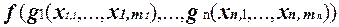h, т.е. S -это замкнутый класс.

Лемма (О несамодвойственной функции)

Если f 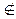S, то подстановкой вместо переменных этой функции функций x и 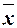можно получить одну из функций констант.