Доказательство
Пусть N = ((V, U), c) - некоторая транспортная сеть.
Последовательность Н = x1, ... , xk разных вершин этой сети называется цепью, если
"i= 1, . . . , k- 1((xi, xi+1)ÎU Ú (xi+1, xi )ÎU).
То есть любые две соседние вершины цепи соединяются между собой ребром одним из двух возможных способов. При этом, если (xi, xi+1)ÎU, то такое ребро называется прямым. Если же (xi+1, xi)ÎU, то такое ребро называется обратным.
Множество всех прямых и обратных ребер цепи Н обозначается как U(H). Множества прямых и обратных ребер той же цепи обозначаются какU+(H) иU-(H) соответственно.
Построим по шагам поток y в транспортной сети N.
1. Положим i = 0 и методом насыщения дуг построим некоторый полный поток yi в сети N.
2. Пока это возможно, повторяем следующие действия.
2.1. Найдем цепь Н = x1, x2, . . . , xk -1, xk, где I= x1 и S= xk,для которой выполняются условия:
" u ÎU+(H) (yi(u) < c(u)); (1)
" u ÎU-(H) (yi(u) > 0). (2)
2.2. Если такая цепь Hнайдена, то вычислим значения:
d1 = min(c(u)- yi(u)), где u ÎU+(H).
d2 = min(c(u)), гдеu ÎU-(H).
d = min(d1,d2).
(Заметим, чтоd является целым числом и d > 0.)
2.3.Определим функцию yi+1 следующим соотношением:
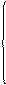y(u)+d, если u ÎU+(H)
yi+1(u) = y(u)-d, если u ÎU-(H)
y(u), если u ÏU(H).
3. Увеличим значение i на 1.
Действие 2 в приведенной процедуре повторяется конечное число раз, поскольку на всяком шаге величина новой функции yi+1 на одном из ребер, ведущих в сток сети, увеличивается на целое число d> 0. Поэтому число повторений выполнения действия 2 не превышает суммы пропускных способностей всех ребер, ведущих в S.
Пусть yk- последняя из функций, определяемых при выполнении приведенной процедуры. Положим y= yk.
Покажем, что y является максимальным потоком в сети N.
1. y является потоком, поскольку если некоторая функция yi - это поток, то действие 2по потоку yi определяет новый поток yi+1.
Действительно, при определении yi+1 значения потока изменяются только для ребер из U(H). При этом поток в прямых ребрах возрастает, а в обратных убывает на такую величину, что новое значение для каждого ребра сети не превосходит пропускную способность этого ребра и не становится отрицательным. Поэтому для yi+1 выполняется первое условие определения потока в сети.
Для всякой внутренней вершины цепи Hсохраняется равенство суммарных входного и выходного потоков.
Действительно, пусть aj - внутренняя вершина из H.
Рассмотрим возможные случаи прохождения ребер из U(H) через вершину aj
1. aj-1aj a j+1
 |
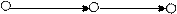При этом входящий и выходящий потоки вершины aj увеличиваются на d.
2.aj-1aj aj+1
 |
В этом случае входящий поток для вершиныaj по одному входному ребру возрастает на d, а по другому входному ребру убывает на d, а его величина оказывается неизменной, совпадающей с выходным потоком этой вершины.
aj-1aj aj+1
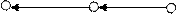3.
Входящий и выходящий потоки для aj уменьшаются на d, оставаясь равными.
aj-1aj aj+1
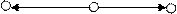4.
Выходящий поток вершины aj по одному ребру возрастает на d, а по другому ребру убывает на d.
Во всех случаях суммарный входящий поток вершины aj для yi+ 1 остается равным суммарному выходящему потоку этой вершины, если такое равенство имеет место для yi. Поэтому для yi+1 выполняется и второе условие определения потока в сети.
2. Покажем, что y является максимальным потоком.
2.1. Обозначим как R - множество таких вершин сети N, что a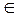 
R тогда и только тогда, когда для всякой цепи H, начинающейся в истоке I и заканчивающейся в a, не выполняются условия
" u ÎU+(H) (yi(u) < c(u)) (1)
" u ÎU-(H) (yi(u) > 0) (2)
Множество R является непустым, так как из определения функции y следует, что SÎR.
Множество остальных вершин сети обозначим F. Так как для Iвыполнены условия (1) и (2). Действительно, единственная цепь, ведущая из I в I, состоит из вершины I. Для этой цепи выполняются условия (1) и (2).ЗначитI 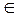F и F не является пустым множеством.
2.2. Обозначим как L множество ребер сети N, начала которых принадлежат множеству F, а концы - множеству R.
Всякий путь W из Iв Sсодержит хотя бы одно ребро из L, поскольку его начало лежит в F, а конец - в R. Следовательно, в последовательности W содержатся две последовательно идущие вершины a и b, для которых aÎF и bÎR.Поэтому L образует сечение сети N.
2.3. Все ребер сечения L справедливо свойство:
"uÎL(y(u) = c(u)).
То есть все ребра L полностью нагружены потоком. В противном случае, если ребро u= (a,b),является недогруженным, то вершина bтакого ребра из L, не может принадлежать R.
Действительно, если y(u) < c(u), то найдется цепь, ведущая в b, которая проходит через u, в которой все прямые ребра недогружены, а по обратным ребрам течет ненулевой поток. Такая цепь может быть получена добавлением вершины b к цепи, ведущей в a, для которой выполнены условия (1) и (2). Последнее ребро для такой цепи является прямым и оно недогружено.Поэтому bÎF, а это противоречит предположению, что bÎR.
2.4. Если u = (a, b) - это ребро, для которого a 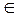R и
b 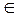F, то y(u) = 0.
Чтобы убедиться в справедливости последнего свойства, предположим противное: существует такое ребро u = (a, b), что a 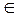R, b 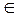Fиy(u) > 0.
Тогда, так как b 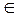F, то существует цепь H = I, . . . , b, для которой выполнены условия (1) и (2). Но тогда эти же условия выполнены и для цепи H* = I, ... , b, a. Поскольку в ней вершины a иb связаны обратным ребром, по которому течет ненулевой поток.
Поэтому a 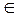F,что противоречит предположению о том, что a 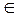R.
Следовательно, поток между вершинами множеств F и R может протекать лишь в одном направлении.
2.5. Поэтому суммарный поток, проходящий через ребра сечения L, в дальнейшем распространяется только между вершинами множества R и полностью входит в сток S.
Следовательно, справедливо соотношение y(N) = c(L).
То есть y - это максимальный поток, так как его величина совпадает с пропускной способностью сечения L,величину которого не превосходит ни один поток в сети.
Дата добавления: 2015-09-18; просмотров: 611;