Доказательство. Пусть N = (G, c) - это произвольная транспортная сеть

Пусть N = (G, c) - это произвольная транспортная сеть. Рассмотрим последовательность рациональнозначных функций пропускной способности ребер сети N: c₁, . . . , c_i, . . . , которые равномерно сходятся к функции c снизу.

Из следствия 2 следует, что для транспортных сетей
N_i = (G, c_i), i = 1, ... существуют максимальные потоки

y₁, . . . , y_i, . . . (1)

Пусть сеть N содержит ребра u₁, ... , u_m.

Из последовательности (1) выделим такую бесконечную подпоследовательность потоков

y_1,1 . . . , y_1,j, . . . (2),

что числовая последовательность y₁,_i(u₁), i = 1, 2, . . .
является сходящейся.

Из последовательности (2) выделим подпоследовательность

y₂,₁, . . . , y₂,_j . . . (3).

Для (3) числовая последовательность y₂,_j (u₂), j= 1, 2, . . .также является сходящейся.

Продолжая процесс выделения подпоследовательностей, через конечное число шагов получаем последовательность функций

y_m,₁, ... , y_m,_j, . . . (m).

Эта последовательность состоит из потоков, значения которых на каждом ребре сети образуют сходящиеся последовательности.

Пусть y .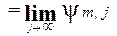

1. Покажем, что y является потоком.

Поскольку для всякого потока y_m,_j справедливо неравенство

y_m,_j 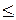c_m,j, то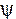 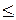c.

Кроме того, для всякого потока y_m,_j и внутренней вершины aсети N_m,_jвыполняется равенство

.

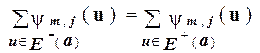Предельный переход по j ® ¥ преобразует последнее равенство в равенство

.

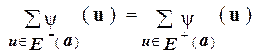Следовательно, y является потоком в N.

2. Покажем, что y - это максимальный поток.

Если c_m,_j - функция пропускной способности, отличающаяся от cна всех ребрах сети не более чем на e, то величина всякого потока в транспортной сети N не превосходит величины y + k´ e, где k - число ребер, выходящих из истока сети.

Поскольку значение e можно выбрать сколь угодно малым, то величина всякого потока в N не превосходит значения величины потока y. Следовательно, y - это максимальный поток.

Доказательство окончено.