МОНОТОННЫЕ ФУНКЦИИ

На множестве двоичных наборов длины n определим отношение предшествования наборов.

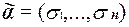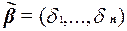Пусть и . Тогда набор 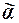предшествует набору 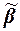, если .

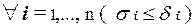Отношение предшествования наборов обозначается как 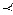, т.е. значение каждой компоненты предшествующего набора не превосходит значения соответствующей компоненты следующего набора.

Например, наборы (0, 1, 0, 0, 1, 0) и (0, 1, 1, 0, 1, 1) находятся в отношении предшествования, а наборы
(1, 1, 0, 0, 1, 0) и (1, 0, 1, 0, 1, 1) оказываются несравнимыми в отношении .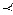

Упражнение. Проверить, что отношение предшествования наборов является отношением частичного порядка.

Рассмотрим представление отношения 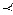на множестве 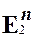с помощью диаграммы для этого отношения, представленной на рис 4.6. Пусть n = 3.

1 1 1

0 1 1 1 0 1 1 1 0

1 0 0 0 1 0 0 0 1

0 0 0

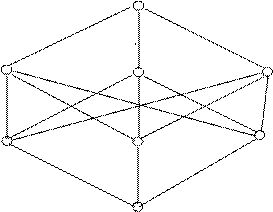
Рис. 4.6

На приведенной диаграмме не указана ориентация дуг, которые всегда считаются ориентированными в направлении верхней из двух вершин, соединяемых дугой.

Все наборы единичного n-мерного куба, имеющие равное число единиц, несравнимы между собой и образуют слой в таком кубе. В случае произвольного значения n в диаграмме для отношения 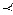содержится n +1 слоев.

Упражнение. Нарисовать диаграмму отношения 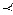для
n = 4.