ЛИНЕЙНЫЕ ФУНКЦИИ
Напомним, что линейными называются функции, представимые в виде 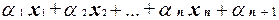 , где a1, . . . , an+1 - двоичные коэффициенты при переменных и свободном члене, равном 1.
, где a1, . . . , an+1 - двоичные коэффициенты при переменных и свободном члене, равном 1.
Класс линейных функций обозначается как L.
Из установленного способа представления линейных функций следует, что существует ровно 2n+1 различных линейных функций, зависящих от n переменных. Действительно, записи линейных функций являются частным случаем полиномов Жегалкина, поэтому представление всякой линейной функции в виде 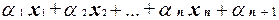 единственное. Поэтому линейных функций от n переменных ровно столько, сколько имеется способов составления различных записей вида:
единственное. Поэтому линейных функций от n переменных ровно столько, сколько имеется способов составления различных записей вида: 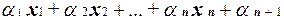 .
.
Класс L является замкнутым, поскольку преобразование всякой суперпозиции линейных функций к виду полинома Жегалкина не приводит к появлению нелинейных слагаемых.
Замечание. Только две линейные функции n переменных существенно зависят от всех своих переменных:
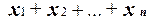 и
и 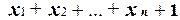 .
.
Всякая другая линейная функция n переменных, полином Жегалкина для которых не содержит вхождения некоторых переменных, имеет несущественные переменные.
Все 4 функции одной переменной: 0, 1, x и 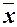 являются линейными.
являются линейными.
Простейшим примером нелинейной функции можно считать x1&x2, поскольку ее представление в виде полинома Жегалкина содержит одно произведение переменных. Покажем, что эта простейшая нелинейная функция может быть выражена из любой нелинейной функции.
Лемма (О нелинейной функции)
Если f(x1, . . . , xn) 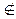 L, то подстановкой вместо переменных этой функции функций-констант 0, 1, тождественных функции x и отрицанию
L, то подстановкой вместо переменных этой функции функций-констант 0, 1, тождественных функции x и отрицанию 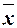 , а также применением отрицания к f можно получить функцию
, а также применением отрицания к f можно получить функцию 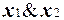 .
.
Дата добавления: 2015-09-18; просмотров: 704;
