Алгоритм исследования функции на экстремум с помощью второй производной

1 Найти первую производную функции .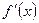

2 Приравнять ее к нулю, найти действительные корни полученного уравнения ( т.е. критические точки ( ).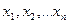

3 Найти вторую производную .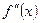

4 Во вторую производную подставить поочередно все критические значения; если при этой подстановке вторая производная окажется положительной, то в этой точке функция имеет минимум; если же вторая производная окажется отрицательной, то функция имеет максимум.

6Определить промежутки выпуклости и вогнутости функции и точки перегиба.

Правило нахождения интервалов выпуклости функции и точек перегиба

1 Найти вторую производную функции и точки, в которых она равна нулю или не существует.

2 Определить интервалы, на которые область определения разбивается найденными точками.

3 Установить знаки второй производной в каждом из указанных интервалов. Если 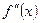<0,то в рассматриваемом интервале кривая выпукла; если 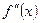>0 – вогнута. Изменение знака указывает на наличие точки перегиба.

4 Найти ординаты точек перегиба.

7Найти точки разрыва (если они есть) и асимптоты.

8Используя результаты исследования, соединить полученные точки плавной кривой. Иногда для большей точности графика находят несколько дополнительных точек, их координаты вычисляют, пользуясь уравнением кривой.