Решение. Исследуем функцию на экстремум

Исследуем функцию на экстремум. Если точки экстремума принадлежат данному отрезку, то вычисляем значения функции в точках экстремума и на концах отрезка и выбираем из них наибольшее и наименьшее

y’=2x-3x²;

2x-3x²=0; x(2-3x)=0

х₁=0; x₂= 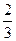– критические точки, причем обе принадлежат отрезку [-1;3]. Вычислим значения функции:

f(0)=0, f(-1)=2, f(3)=-18, f(2/3)=4/27

Ответ:f_наиб.=2, f_наим.= -18.

№ 7 Найдите вторую производную функции 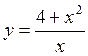и вычислите f’’(4).